Основное уравнение спиральных механизмов с окружной орбитой

Для окружной орбиты шаг t связан с эксцентриситетом 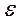и толщиной ребра 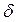спирали следующими зависимостями.

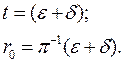
Эти зависимости являются основными уравнениями спиральных механизмов с окружной орбитой взаимно огибаемых спиралей. Они устанавливают связь между эксцентриситетом, толщиной ребра и основной окружностью спиралей.

Кривая Архимеда образуется точкой 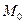при качении без проскальзывания прямой NK по основной окружности 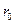. Уравнение аналитической кривой в полярной системе координат имеет вид (Рисунок 74).

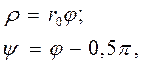
где 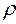- радиус-вектор; 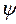- полярный угол.

Точка касания линии 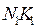с основной окружностью-точкой P-является мгновенным полюсом скоростей. Через полюс проходит нормаль 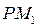к спирали в точке 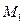. Продолжение этой нормали до точки 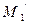- представляет собой нормаль ко второй, внешней ветви спирали. Это важное отличие спирали Архимеда от эвольвенты.

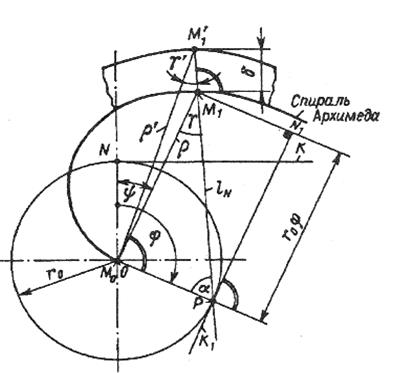
Рисунок 74 – Расчет СПК со спиралями Архимеда