Моменты инерции твердых тел
Для исследования вращательного движения вводится понятие моментов инерции. Как масса является мерой поступательного движения механической системы, так моменты инерции — мерой вращательного движения. Момент инерции механической системы относительно оси 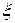 вычисляется по формуле
вычисляется по формуле
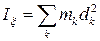 ,
,
где 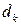 — расстояние от точки массой
— расстояние от точки массой 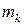 до оси
до оси 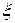 .
.
При вычислении моментов инерции сплошных твердых тел сумму заменяют интегралом
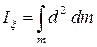 .
.
Моменты инерции одинаковых по форме однородных тел, изготовленных из разных материалов, отличаются друг от друга. Характеристикой, не зависящей от массы материала, является радиус инерции 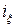 относительно оси
относительно оси 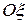 . Момент инерции относительно оси в этом случае определяется по формуле
. Момент инерции относительно оси в этом случае определяется по формуле
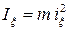 .
.
При решении конкретных задач очень полезна бывает теорема Штейнера, позволяющая найти момент инерции тела относительно оси 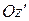 , если известна величина момента инерции того же тела относительно оси проходящей через центр масс
, если известна величина момента инерции того же тела относительно оси проходящей через центр масс 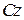 и расстояние от новой оси до оси, идущей параллельно ей через центр масс
и расстояние от новой оси до оси, идущей параллельно ей через центр масс 
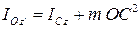 .
.
Встречаются такие задачи, в которых момент инерции относительно оси вращения 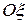 неизвестен, но известны моменты инерции этого тела относительно других осей, которые можно связать с некоторой координатной системой (например: декартовых
неизвестен, но известны моменты инерции этого тела относительно других осей, которые можно связать с некоторой координатной системой (например: декартовых 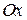 ,
, 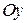 ,
, 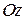 в случае описания вращательного движения ротора с неточно установленной осью вращения). В этом случае момент инерции, относительно оси
в случае описания вращательного движения ротора с неточно установленной осью вращения). В этом случае момент инерции, относительно оси 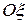 , составляющей с декартовой системой координат
, составляющей с декартовой системой координат 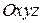 углы
углы 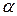 ,
, 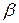 ,
, 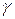 можно определить по формуле
можно определить по формуле
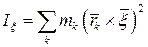 ,
,
где 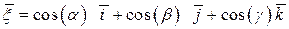 — единичный вектор, характеризующий направление оси
— единичный вектор, характеризующий направление оси 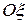 относительно декартовой системы координат;
относительно декартовой системы координат;
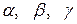 — углы между осью
— углы между осью 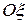 и координатными осями
и координатными осями 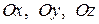 .
.
Дата добавления: 2015-08-08; просмотров: 1183;
