Пара сил. Момент пары
Две равные по величине и противоположно направленные силы образуют пару сил, если линии их действия не совпадают (рис.2.17).
Пара сил характеризуется плоскостью действия, направлением вращательного действия, величиной момента пары.
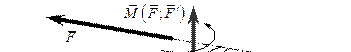
Рис.2.17 Пара сил, момент пары
 Силы пары не образуют уравновешенную систему сил, хотя геометрическая сумма сил пары равна нулю.
Силы пары не образуют уравновешенную систему сил, хотя геометрическая сумма сил пары равна нулю.
Сумма моментов сил, составляющих пару, не зависит от выбора центра и равна произведению силы пары на плечо пары.
Докажем эту теорему: пусть в плоскости "П" действует пара сил ( 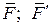 ). Определим вектор-момент пары, как сумму моментов каждой из сил, относительно одного и того же центра О, выбранного произвольно. Учтем, что силы пары противоположны по направлению
). Определим вектор-момент пары, как сумму моментов каждой из сил, относительно одного и того же центра О, выбранного произвольно. Учтем, что силы пары противоположны по направлению 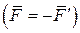 . Радиусы- векторы точек приложения сил пары относительно центра
. Радиусы- векторы точек приложения сил пары относительно центра 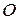 связаны очевидным соотношением
связаны очевидным соотношением
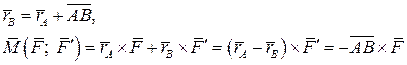
или 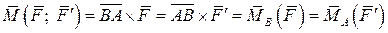

Полученный вектор является моментом пары. Его модуль равен произведению силы пары на расстояние между линиями действия сил пары (см. рис.), называемое плечом пары
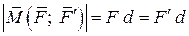
Дата добавления: 2015-08-08; просмотров: 800;
