Напряжения. Метод сечений позволяет определить величину внутреннего си­лового фактора в сечении, но не дает возможности установить за­кон распределения внутренних сил по

Метод сечений позволяет определить величину внутреннего си­лового фактора в сечении, но не дает возможности установить за­кон распределения внутренних сил по сечению. Для оценки прочно­сти необходимо определить величину силы, приходящуюся на любую точку поперечного сечения.

Величину интенсивности внутренних сил в точке поперечного сечения называют ме-ханическим напряжением. Напряжение характеризует величину внутренней силы, при-ходящейся на единицу пло­щади поперечного сечения.

Рассмотрим брус, к которому приложена внешняя нагрузка (рис. 19.2). С помощью метода сечений рассечем брус поперечной плоскостью, отбросим левую часть и рассмотрим равновесие остав­шейся правой части. Выделим на секущей плоскости малую площад­ку ΔА На этой площадке действует равнодействующая внутренних сил упругости.

Направление напряжения р_ср совпадает с направлением внутренней силы в этом сече­нии.

Вектор р_ср называют полным напряжени­ем. Его принято раскладывать на два вектора (рис. 19.3):

τ — лежащий в площадке сечения и

σ — направленный перпендикулярно площад­ке.

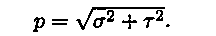
Если вектор р — пространственный, то его раскладывают на три составляющие:

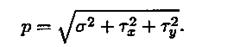
Нормальное напряжение характеризует сопротивление сечения растяжению или сжатию.

Касательное напряжение характеризует сопротивление сечения сдвигу.

Сила N (продольная) вызывает появление нормального

напря­жения σ.

Силы Q_x и Q_y вызывают появление касательных напря­жений τ. Моменты изгибающие М_х и М_у вызывают появление нор­мальных напряжений σ, переменных по сечению.

Крутящий момент M_z вызывает сдвиг сечения вокруг продоль­ной оси, поэтому появляются касательные напряжения τ.

ЛЕКЦИЯ 20

Тема 2.2. Растяжение и сжатие.