Математические основы векторной графики

Рассмотрим подробнее способы представления различных объектов в векторной графике.

Точка.Этот объект на плоскости представляется двумя числами (х, у), указывающими его положение относительно начала координат.

Прямая линия.Ей соответствует уравнение у = kх + b. Указав параметры k и b, всегда можно отобразить бесконечную прямую линию в известной системе координат, то есть для задания прямой достаточно двух параметров.

Отрезок прямой.Он отличается тем, что требует для описания еще двух параметров — например, координат х₁ и х₂ начала и конца отрезка.

Кривая второго порядка.К этому классу кривых относятся параболы, гиперболы, эллипсы, окружности, то есть все линии, уравнения которых содержат степени не выше второй. Кривая второго порядка не имеет точек перегиба. Прямые линии являются всего лишь частным случаем кривых второго порядка. Формула кривой второго порядка в общем виде может выглядеть, например, так:

x² + а₁у² + а₂xу + а₃x + а₄у + а₅ = 0.

Таким образом, для описания бесконечной кривой второго порядка достаточно пяти параметров. Если требуется построить отрезок кривой, понадобятся еще два параметра.

Кривая третьего порядка.Отличие этих кривых от кривых второго порядка состоит в возможном наличии точки перегиба. Например, график функции у = x³ имеет точку перегиба в начале координат (рис. 15.5). Именно эта особенность позволяет сделать кривые третьего порядка основой отображения природных объектов в векторной графике. Например, линии изгиба человеческого тела весьма близки к кривым третьего порядка. Все кривые второго порядка, как и прямые, являются частными случаями кривых третьего порядка.

В общем случае уравнение кривой третьего порядка можно записать так:

x³ + а₁у³ + а₂x²у + а₃ху² + а₄x² + а₅у² + а₆ху + а₇х + а₈y + а₉ = 0

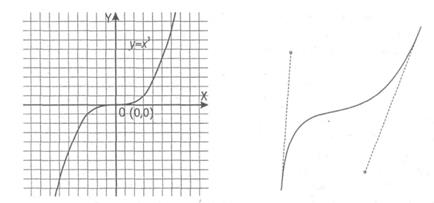
Рис. 5. Кривая третьего порядка (слева) и кривая Безье (справа)

Таким образом, кривая третьего порядка описывается девятью параметрами. Описание ее отрезка потребует на два параметра больше.

Кривые Безье.Это особый, упрощенный вид кривых третьего порядка (см. рис. 15.5). Метод построения кривой Безье основан на использовании пары касательных, проведенных к отрезку линии в ее окончаниях. Отрезки кривых Безье описываются восемью параметрами, поэтому работать с ними удобнее. На форму линии влияет угол наклона касательной и длина ее отрезка. Таким образом, касательные играют роль виртуальных «рычагов», с помощью которых управляют кривой.