Интервал. В обычном пространстве расстояние Dl между двумя точками с координатами xi, у1, z1 и x2, у2, z2

В обычном пространстве расстояние Dl между двумя точками с координатами x_i, у₁, z₁ и x₂, у₂, z₂. определяется выражением

,

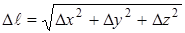где Dx = x₂ ‑ x₁ и т. д. Это расстояние не зависит от выбора системы координат, т. е. является инвариантом. При переходе к другой координатной системе изменяются, вообще говоря, величины Dx, Dy и Dz, однако эти изменения таковы, что расстояние Dl остается одним и тем же.

Казалось бы, что расстояние (или, как принято говорить, интервал) между двумя мировыми точками в четырехмерном пространстве-времени должно определяться аналогичным выражением

,

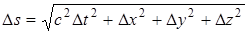где Dt = t₂ ‑ t₁ и т. д. Однако это выражение непригодно в качестве интервала, поскольку оно не является инвариантом — при переходе к другой инерциальной системе отсчета числовое значение этого выражения изменяется. Инвариантным, как мы покажем, является выражение

,

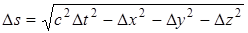которое называют интервалом между событиями. Величина Ds является аналогом расстояния Dl между точками в обычном пространстве.

Причина того, что интервал определяется не выражением
…………. ,
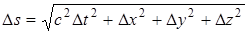а выражением
………… ,
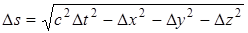заключается в том, что, как говорят, метрика пространства-времени отличается от метрики обычного трехмерного пространства. В обычном пространстве справедлива евклидова геометрия, вследствие чего его называют евклидовым. Качественное различие между временем и пространством приводит к тому, что в выражение для интервала квадрат временной координаты и квадраты пространственных координат входят с разными знаками. Пространство, в котором расстояние между точками определяется выражением вида 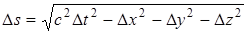, называется псевдоевклидовым. Его можно написать в виде

,

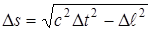где Dl — расстояние между точками обычного пространства, в которых произошли данные события.

Допустим, что рассматриваются события, происходящие с одной и той же частицей. Тогда отношение Dl/Dt дает скорость частицы v. Поэтому, вынеся из-под корня cDt, получим, что

.

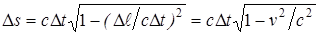Мы получили выражение 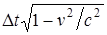. Оно равно Dτ — промежутку собственного времени частицы между событиями. Таким образом, мы приходим к соотношению

Ds = c·Dτ.

Поскольку c — константа, а Dτ—инвариант, интервал Ds также оказывается инвариантом. Убедиться в инвариантности интервала можно еще одним способом……..