Лекция 1. Электростатика.

§ 1 – 1 Электрический заряд.

Электричество как особый вид материи изучалось еще древними греками, но коли-чественная мера его - электрический заряд – была введена лишь после опытов Кулона. Ос-

новным свойством заряда является его дискретность. Наименьший заряд, известный в настоящее время, равен 1,6·10 ^–19 Кулона (единица измерения – Кулон - будет определена позднее). Предполагается, что возможны дробные части этого заряда – кварки, но они до настоящего времени экспериментально не обнаружены. Однако, установлено, что сум-марная величина электрического заряда в доступной нашим наблюдениями части Вселен-ной остается постоянной. Это положение носит название закона сохранения заряда.

Существуют два различных типа электрических зарядов, один из которых по пред-ложению Б.Франклина был назван положительным, а другой – отрицательным. Субъек-тивный характер выбора такого названия привел к тому, что заряд электрона – наиболее известной элементарной частицы – оказался отрицательным. Это, в свою очередь, привело к некоторой путанице в определении направления электрического тока, но на первой стадии изучения электричества нас будут интересовать неподвижные заряды, обычно называемые статическими.

§ 1 – 2 Закон Кулона.

Еще из школьного курса физики известно, что электрические заряды взаимодейст-вуют друг с другом. Величина силы взаимодействия измерена Кулоном, и закон, харак-теризующий силу взаимодействия двух статических точечных зарядов Q и q, носит его имя. Если учесть, что сила – это вектор, то этот закон может быть записан в таком виде:

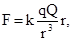
где r /r – единичный вектор, направленный вдоль прямой, соединяющей оба заряда, расстояние между которыми равно r.

Коэффициент k вводится в связи с использованием определенной системы единиц. В принятой у нас системе СИ этот коэффициент выражается через так называемую диэлек-трическую постоянную вакуума ε₀ = 8,86 · 10 ^–12 Ф/М ( k = 1/ 4π ε₀). Причиной появления этого коэффициента является выбор единицы измерения заряда – в системе СИ заряд измеряется в Кулонах, являющихся производными единицами ( основной единицей служит Ампер – единица измерения силы тока).

Замечание: понятие точечного заряда является математической абстракцией, в действи-тельности приходится иметь дело с зарядами, заполняющими либо некоторый объем, либо некоторую площадь, а иногда – в случае тонких длинных проводов – некоторую длину. Как правило, заряды распределяются неравномерно, поэтому можно рассматривать объемную, поверхностную или линейную плотности зарядов, определяемые как:

; ;

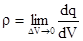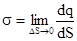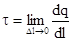
где dV,dS и dl – бесконечно малые элементы объема, площади и длины соответственно.Ве-личина бесконечно малого заряда, который можно рассматривать как точечный, при этом определяется как dq₁= ρdV,dq₂ = σdS, dq₃ = τdl.

§ 1 – 3 Напряженность электрического поля.

В предыдущем разделе (механике) отмечалось, что любое взаимодействие тел, нахо-

дящихся на некотором расстоянии друг от друга, осуществляется посредством поля. При-менительно к электрическим зарядам это означает, что вокруг любого заряда существует особый вид материи – электрическое поле. Это поле не воспринимается непосредственно чувствами человека. Для обнаружения поля используются другие заряды, называемые пробными. Однако, из закона Кулона следует, что величина силы воздействия на пробный заряд зависит от величины этого заряда. Для характеристики самого поля вводится вели-чина силы, действующей на пробный заряд, отнесенная к величине этого пробного заряда. Эта величина называется напряженностью электрического поля. Другими словами можно сказать, что напряженность электрического поля есть сила, действующая на единич-ный положительный заряд, помещенный в данную точку поля.Если обозначить заряд, поле которого мы изучаем – Q, то напряженность поля в любой точке пространства вокруг этого заряда, находящейся на расстоянии r от него, равна:

E=(1/4pe) (Qr) /r³ ; E = (1/4pe)(Q/r²).

Напряженность поля от нескольких зарядов находится по принципу суперпозиции: напря-женность поля от суммы зарядов равна сумме всех напряженностей от каждого заряда в от-дельности, т.е. E (Σ Q_i) = Σ (E_i).

Этот принцип позволяет находить напряженность поля от любых зарядов, распреде-ленных в пространстве, причем, вместо суммы используются интегралы. Однако вычисле-ние осложняются тем, что напряженность поля – вектор. Поэтому часто приходится сначала вычислять отдельные составляющие вектора Е, а общую величину находить их суммированием. Для прямоугольной системы координат это делается сравнительно просто:

E² = E_x² + E_y² +E_z².

Простой пример: найти напряженность электрического поля, которую создает бесконечная нить, равномерно заряженная по длине с линейной плотностью τ. Для решения этой задачи необходимо найти поле от бесконечно малого (точечного) заряда dq и затем произвести суммирование по всей длине нити. Поле от заряда dq на расстоянии r от него (см.рис.1) рав-

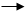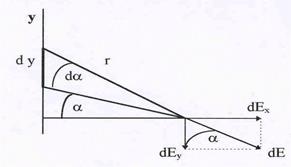Рис.1 Вычисление поля от бесконеч-ной нити.

но dE = (1/4pe)(dq/r2), dE = dEx + dEy;   dEx = dEcosα ; dEy = dEsinα ;   Ex = ò dEx , Ey = òdEy. Для суммирования (интегрирования в нашем случае) удобно ввести одну переменную, а ос-тальные связать с ней при помощи геометри-ческих соотношений. За такую переменную можно взять угол a. Тогда r = x/cosa, y/x0 = tga.

Из последнего соотношения следует (dy/x₀) = da/cos²a.

E_x = =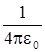

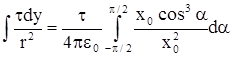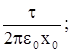
E_y = 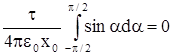. Ответ : Е = .

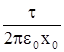Из приведенного примера следует, что принцип суперпозиции позволяет вычислить напряженность поля от любой конфигурации зарядов, представив ее как некую сумму бес-конечно малых (точечных) зарядов. Дело лишь в том, как проводить суммирование (интег-рирование). Для рассмотренного одномерного случая это простой интеграл. Для распре-деления зарядов по поверхности это будет двумерный (поверхностный) интеграл, для объемного распределения – трехмерный (объемный) интеграл. Для наглядного представ-ления электрическое поле принято изображать в виде линий, названных силовыми. Под си-ловыми линиями понимаются линии, касательные к которым в данной точке совпадают с направлением вектора напряженности в этой точке. Кроме того, было условлено, что гус-тота силовых линий должна быть пропорциональна величине напряженности. Силовые линии начинаются на положительных и кончаются на отрицательных зарядах. Картина силовых линий от двух точечных зарядов изображена на рис.2. Как видно из рисунка, в промежутке между зарядами силовые линии являются непрерывными.

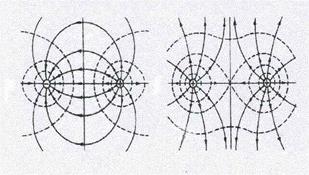Рис.2 Линии напряженности.

Это означает, что направление векторов напряженности во всех точках однозначно, т.к. линии нигде не пересекаются. Для количественного описания силовых линий вводится понятие потока. Потоком вектора напряженности через за-данную поверхность называется скаляр-ное произведение вектора напряженности на величину этой поверхности: Ф = (ЕS). При этом предполагается, что поверхность -

– это вектор, причем направление этого вектора определяется направлением внешней нормали n к поверхности, т.е. нормали, проведенной в сторону выпуклости поверхности (см. рис.3): dФ = (E dS) = EdS cosa = E_n dS. Для плоской поверхности направление внешней нормали должно задаваться дополнительными условиями.

§ 1 – 4 Теорема Гаусса.

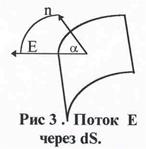
Полный поток вектора напряженности электрического поля через любую замкнутую поверхность с точностью до коэффици-ента 1/e0 равен алгебраической сумме зарядов, находящихся вну-три этой поверхности. Доказательство этого утверждения проводится в три этапа. Сначала теорема доказывается для точечного заряда и выпуклой поверхнос-ти.Затем рассматривается поверхность любой формы, наконец , до-казательство формулируется для системы зарядов.

1. Рассмотрим точечный заряд Q. Опишем вокруг его воображаемую сферу и вычислим полный поток через эту поверхность. Для вычисления используем определение телесного угла dW (см. рис.4):

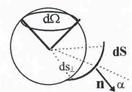Рис.4.Телесный угол.

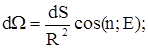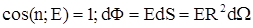; Ф = 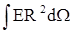= 4p E R2, т.к. в подинтегральном выражении величины E и R, а полный телесный угол равен 4p. Подставляя вместо Е определение напря-женности поля для точечного заряда Q, находим, что

Ф = .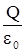

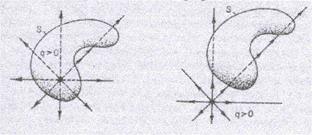Рис.5. Различные формы прверхностей

Видно, что результат не зависит от радиуса сферы. Если поверхность несферическая, но выпуклая, то, как известно из стериометрии, dScosa = dS = dSn (см.рис.4), и вновь ре-зультат оказывается прежним. 2. Если поверхность интегрирования имеет произвольную форму, то для заряда внутри поверхности линии напряженности пересе-

кают ее нечетное количество раз (один или три) (см. рис.5), причем косинус угла между вектором напряженности и внешней нормалью к поверхности будет два раза положитель-ным и один раз отрицательным ( угол a - тупой), так что два слагаемых общего потока компенсируют друг друга.

Если же заряд находится вне поверхности, то поток пересекает ее четное количество раз (два, четыре и т.д) так, что положительные и отрицательные ( для тупых углов между n и Е) слагаемые уничтожают друг друга и общий поток оказывается равным нулю.

3. Если зарядов несколько, то в силу принципа суперпозиции Е (SЕ_i) = S Е_i ; Ф_S = S Ф_i . Для каждого заряда в отдельности теорема доказана, значит она остается справедливой и для макроскопического (конечного) заряда, который можно представить в виде суммы точеч-ных зарядов.

Математическая форма записи теоремы Гаусса имеет следующий вид:

Ф₀ = 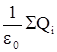или в развернутом виде .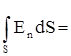

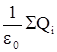Следствие:если заряды, создающие поле, находятся вне воображаемой замкнутой поверх-ности, то поток напряженности через эту поверхность равен нулю.

Теорема Гаусса имеет достаточно важное значение, т.к. является одним из уравнений Максвелла, которые лежат в основе теории электромагнетизма. Кроме того, эта теорема может быть использована для вычисления напряженности. Для этого необходимо, чтобы величину Е можно было вынести из-под интеграла. Это можно сделать, если Е =const на всей поверхности интегрирования. Нетрудно догадаться, что воображаемая замкнутая поверхность должна иметь симметрию, подобную симметрии расположения зарядов. При этом удобно ее выбрать так, чтобы косинус угла между вектором Е и нормалью к поверхно-сти принимал значения либо 1 дибо 0. Таким условиям удовлетворяют три класса симмет-рии: сферическая, цилиндрическая и зеркальная, однако в двух последних случаях необхо-димо пренебрегать краевыми эффектами, т.к. на на краях нарушается распределение силовых линий. Ясно, что для выбора конфигурации поверхности необходимо знать, как направлен вектор Е. Здесь важно учитывать, что для статических зарядов напряженность поля вблизи зарядов должна быть перпендикулярной поверхности области распределения зарядов. В противном случае всегда будет составляющая поля, направленная вдоль поверх-ности распределения, что может вызвать электрический ток, и статическое распределение будет нарушено. Для иллюстрации полезно рассмотреть два примера.

Поле от бесконечной плоскости.

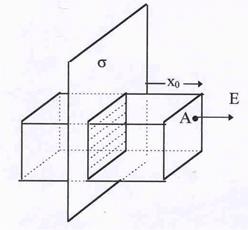Рис.6. Поле от плоскости.

Пусть имеется плоскость, равномерно заряженная с поверхностною плотностью s.Требуется найти напря-женность электрического поля в точке, отстоящей от плоскости на расстояние х0. Для решения задачи про-ведем замкнутую поверхность через заданную точку А (см. рис.6).Поверхность имеет форму прямоуголь-ного параллелепипеда, боковые грани которого пер-пендикулярны заряженной плоскости. Выбор такой формы поверхности связан с тем, что вектор напря-женности электрического поля Е вблизи плоскости должен быть нормален к ней. Кроме того, наша вооб-ражаемая поверхность должна быть симметричной относительно заряженной плоскости. Полный поток через поверхность параллелпипеда складывается из

потоков через его боковую поверхность и потоков через его верхнее и нижнее основания, параллельные заряженной плоскости. Но поток через боковые поверхности равен нулю, т.к. нормали ко всем четырем боковым граням перпендикулярны вектору Е и для них cosa = =cos(n ^E) = 0. В силу симметрии потоки через верхнее и нижнее основания одинаковы так, что полный поток Ф₀ = 2Е_АS. В то же время заряд, находящийся внутри нашей воображаемой поверхности равен заряду на заштрихованном (см.рис.6) участке, т.е. Q = s S. Тогда из теоремы Гаусса следует, что 2Е_АS =(1/e₀) s S, откуда

Е_А = .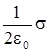

Поле от заряженной сферы.

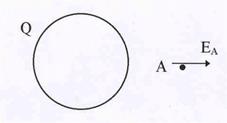Рис.7. Поле от сферы.

В качестве второго примера рассмотрим поле от заря-женной сферы, полный заряд которой равен Q. Если точ-ка А (см. рис7) , где требуется определить напряженность, находится вне заряженной сферы, то очевидно в качестве воображаемой поверхности выбрать сферу, концентри-ческую нашей заряженной сфере. В этом случае ЕА па-раллельно n, и Ф0 = ЕАS.Т.к.площадь сферы равна 4pR2, то из теоремы Гаусса нетрудно найти:

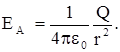
§ 1 – 5. Работа по перемещению заряда в электрическом поле.

Как уже отмечалось, на электрический заряд q со стороны поля, созданного зарядом Q,

действует кулоновская сила. Поэтому при перемещении заряда q в поле совершается рабо-та,величина которой определяется выражением dA = F_ldlcosa, где a - угол между направ-

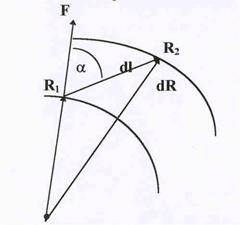Рис.8. К расчету элементарной работы.

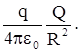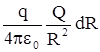лениями силы и перемещения (см. рис 8).Учитывая, что Fcosa = Fl имеем dA = Fldl. Для нашего случая F = qE; qE = Из рис. видно, что dlcosa =dR, и малая работа в поле равна dA = ; A = 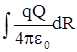= 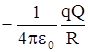. Из полученной форулы следует, что работа по пере-мещению заряда в поле не зависит от формы пути, т.е. электростатические силы являются потенциальными. Следовательно, заряд в поле обладает потенциальной энергией. Работа при изменении расстояния от R1 до R2 равна

= .

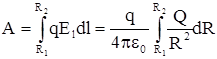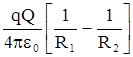Из независимости работы от формы пути перемещения следует, что работа электро-статических сил по замкнутому пути равна нулю. В этом случае в первом интеграле величину заряда q, вынесенную за знак интегрирования, можно сократить. Тогда

.

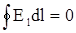В этой формуле интеграл с кружком обозначает так называемую циркуляцию, т.е. он обоз-начает, что интегрировапние проводится по замкнутому контуру. Справедливость этого утверждения следует из непосредственного выражения для элементарной работы при прод-

вижении вдоль элементарного перемещения dl: dA = Edlcosa =E_l dl, где a - угол между направлением силы и перемещения.