Графики подачи. Способы уменьшения неравномерности подачи

Рассматривая схему насоса (см. рис. 1), можно отметить, что поршень перемещается в цилиндре между крайними положени­ями - так называемыми мертвыми точками, скорость движения в ко­торых равна нулю. Перемещение координаты х поршня определяется углом aповорота махо­вика и выражается известным­ из механики уравнением:

x = r(1 – cos a) (11)

Текущая скорость пере­мещения координаты х выра­жается первой производной:

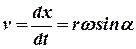, (12)

а текущее значение уско­рения - второй производ­ной:

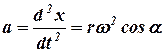, (13)

где 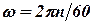- угловая скорость.

Текущее значение подачи жидкости равно произведе­нию скорости поршня на его площадь:

Q_т = Srw sin a. (14)

Таким образом, из формулы (12) видно, что подача жид­кости изменяется по синусоидальному закону, т. е. при a, равном 0, 180°, 360° и т. д., Q_т = 0, а при a, равном 90°, 270° и т. д., Q_т достигает максимальных значений.

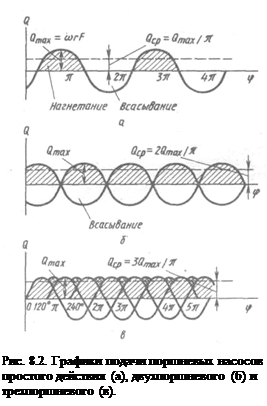
Графически это отражено на рисунке 2, а. Из графика видно, что насос простого действия имеет весьма неравномерную пода­чу. Степень неравномерности d_н, представляющая собой отноше­ние максимального расхода к среднему, для данного насоса составит:

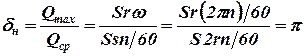. (15)

Неравномерность подачи может быть существенно уменьшена путем увеличения числа цилиндров насоса, поршни которых наса­живаются на общий вал, а кривошипы располагаются под углом друг к другу (по аналогии с двигателем внутреннего сгорания).

Так, на рисунке 2, б представлен график подачи двухпорш­невого насоса. Видно, что максимальная подача Q_max не измени­лась, a Q_cp увеличилась в 2 раза. Поэтому коэффициент неравно­мерности подачи также уменьшился в 2 раза:

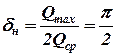. (16)

В трехпоршневом насосе кривошипы отдельных цилиндров сдви­гаются на 120°. Поэтому на графике подачи (рис. 2, в) при одинаковых максимальных расходах общая подача возрастает в 3 раза, а неравномерность подачи значительно уменьшается; коэф­фициент неравномерности при этом практически равен единице:

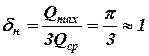. (17)

В целях уменьшения неравномерности подачи поршневых насосов возможны и другие конструктивные решения: установка воз­душных колпаков, применение насосов дифференциального типа, двойного действия и др.