Уравнение гармонического колебательного движения.
Пусть на некоторое тело массы “m” действует квазиупругая сила 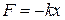 , под действием которой тело приобретает ускорение “a”, тогда по II-закону Ньютона
, под действием которой тело приобретает ускорение “a”, тогда по II-закону Ньютона 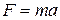 и, следовательно
и, следовательно 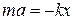 (пример, колебание шарика, подвешенного к пружинке). Здесь движение (колебательный процесс) происходит вдоль оси “x”.
(пример, колебание шарика, подвешенного к пружинке). Здесь движение (колебательный процесс) происходит вдоль оси “x”.
Далее 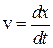 ; и
; и 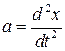 ; тогда
; тогда 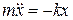 или
или 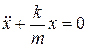 .
.
Колебательный процесс возможен, если коэффициент при “x” положителен, представим его в виде 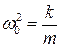 (здесь w0 – вещественная величина). Тогда получим:
(здесь w0 – вещественная величина). Тогда получим:
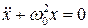
| – дифференциальное уравнение гармонического колебания. |
Таким образом, движение шарика на пружинке под действием силы 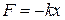 описывается линейным однородным дифференциальным уравнением 2-го порядка.
описывается линейным однородным дифференциальным уравнением 2-го порядка.
Решением такого уравнения является функция вида:
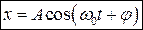 , (8.1)
, (8.1)
где А – амплитуда колебаний, величина наибольшего отклонения системы от положения равновесия. Определяется величиной первоначального отклонения (А = const > 0).
(w0t+j) – фаза колебаний. Физический смысл фазы состоит в том, что она определяет смещение колеблющейся точки в любой момент времени. Постоянная j представляет собой значение фазы в момент времени t = 0 и называется начальной фазой колебания. Из уравнения следует, что фазам, отличающимся на величину, кратную 2p, соответствуют одинаковые смещения.
Так как смещение системы при колебательном движении представляет периодическую функцию от времени, то и скорость и ускорение такой системы будут также в точности повторяться через равные промежутки времени T, за который фаза колебаний получит приращение, кратное 2p. Этот промежуток времени T называется периодом колебаний (или иначе T – это время, за которое совершается полный цикл колебаний).
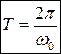 (8.2)
(8.2)
С учетом 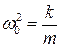 получим
получим
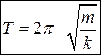 . (8.3)
. (8.3)
Из формулы видно, что период колебаний зависит только от свойств самой системы.
Для описания колебательного периодического движения вводится еще несколько величин:
а) n – частота колебаний – это величина численно равная числу колебаний в единицу времени. 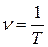 . За единицу частоту (1Гц) принимают частоту такого колебания, период которого равен 1с.
. За единицу частоту (1Гц) принимают частоту такого колебания, период которого равен 1с.
б) w0 = 2pn – круговая или циклическая частота (w0 – число колебаний за 2p секунд).
Для колебательного процесса смещение, скорость и ускорение можно представить как аналитически:
1. 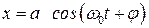 .
.
2. 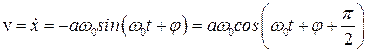 .
.
3. 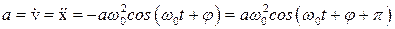 .
.

так и графически (рис. 8.2).
Дата добавления: 2015-08-08; просмотров: 730;
