Кинематика движения материальной точки. Характеристики движения.
Положение материальной точки M в пространстве в данный момент времени может быть задано радиус-вектором 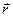 (см. рис. 2.1), соединяющим начало координат выбранной системы отсчета с рассматриваемой точкой. Обозначение: M(x,y,z).
(см. рис. 2.1), соединяющим начало координат выбранной системы отсчета с рассматриваемой точкой. Обозначение: M(x,y,z).
 Линия, которую описывает движущаяся материальная точка в пространстве, называют траекторией. В зависимости от формы траектории движения бывают прямолинейными и криволинейными. (Движение по окружности или по дуге окружности является простейшим случаем криволинейного движения.) Следует знать и помнить, что форма траектории данного движения материальной точки зависит от выбора системы отсчета и в этом смысле оказывается относительной.
Линия, которую описывает движущаяся материальная точка в пространстве, называют траекторией. В зависимости от формы траектории движения бывают прямолинейными и криволинейными. (Движение по окружности или по дуге окружности является простейшим случаем криволинейного движения.) Следует знать и помнить, что форма траектории данного движения материальной точки зависит от выбора системы отсчета и в этом смысле оказывается относительной.
 Пример: Если маленький шарик выпал из окна поезда, движущегося равномерно и прямолинейно по горизонтальному участку, то в системе отсчета, связанной с поездом, шарик опишет вертикальную прямолинейную траекторию. Движение этого же шарика с точки зрения наблюдателя, стоящего на железнодорожной насыпи (система отсчета, связанная с Землей) будет казаться происходящим по криволинейной (параболической) траектории.
Пример: Если маленький шарик выпал из окна поезда, движущегося равномерно и прямолинейно по горизонтальному участку, то в системе отсчета, связанной с поездом, шарик опишет вертикальную прямолинейную траекторию. Движение этого же шарика с точки зрения наблюдателя, стоящего на железнодорожной насыпи (система отсчета, связанная с Землей) будет казаться происходящим по криволинейной (параболической) траектории.
Отрезок траектории ВС (рис. 2.2), пройденный точкой за некоторый промежуток времени, называется длиной пути (или просто путь S).
Вектор перемещения. Движение материальной точки характеризуется вектором перемещения (или просто перемещением), который равен изменению радиус-вектора движущейся точки за рассматриваемый промежуток времени (рис. 2.3). При переходе точки из положения 1 в положения 2 вектор перемещения 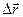 связан с радиус-векторами начального и конечного положения точки соотношением:
связан с радиус-векторами начального и конечного положения точки соотношением: 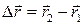 .
.
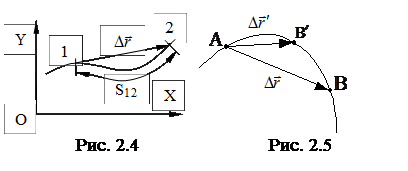 Сравнивая две величины: скалярную – путь S и вектор перемещения
Сравнивая две величины: скалярную – путь S и вектор перемещения 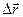 , можно сказать, что для криволинейного движения путь никогда не может равняться модулю вектора перемещения (рис. 2.4).
, можно сказать, что для криволинейного движения путь никогда не может равняться модулю вектора перемещения (рис. 2.4).
Не совпадает путь с модулем вектора перемещения и в случае прямолинейного движения, если направление движения с какого-либо момента времени изменяется на обратное.
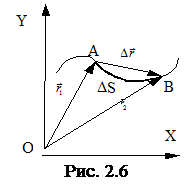 Равенство пути и модуля вектора перемещения имеет место только в одном частном случае: когда прямолинейное движение происходит в одном направлении.
Равенство пути и модуля вектора перемещения имеет место только в одном частном случае: когда прямолинейное движение происходит в одном направлении.
В случае движения по дуге окружности вектор перемещения направлен по секущей, если Dt уменьшать, то величина 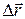 тоже будет уменьшаться, и при Dt®0 секущая будет занимать положение касательной (рис. 2.5). Таким образом, вектор перемещения при криволинейном движении при Dt®0 направлен по касательной в каждой точке.
тоже будет уменьшаться, и при Dt®0 секущая будет занимать положение касательной (рис. 2.5). Таким образом, вектор перемещения при криволинейном движении при Dt®0 направлен по касательной в каждой точке.
Для того, чтобы знать форму траектории движения всего тела в любой момент времени необходимо знать координаты каждой точки тела в каждый момент времени, т.е., необходимо знать как из 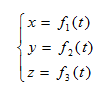 меняются величины (x,y,z) в зависимости от времени. Т.е., требуется определить функции f1, f2, f3. Система уравнений, которая дает возможность определить положение движущегося тела в любой момент времени, называется системой кинематических уравнений движения.
меняются величины (x,y,z) в зависимости от времени. Т.е., требуется определить функции f1, f2, f3. Система уравнений, которая дает возможность определить положение движущегося тела в любой момент времени, называется системой кинематических уравнений движения.
Дата добавления: 2015-08-08; просмотров: 863;
