Космические скорости

Для того, чтобы вывести ракету в космос, ей необходимо сообщить некоторую скорость.

· Скорость, с которой должно двигаться тело m, чтобы удерживаться на орбите вблизи поверхности Земли, называют первой космической скоростью. Эту скорость несложно вычислить с помощью законов динамики.

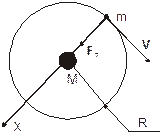
Рис. 2.9. К расчету первой космической скорости.

Второй закон Ньютона для тела m на околоземной орбите (см. рис. 2.9) имеет вид:

.

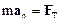Проецируя полученное уравнение на ось Х, имеем:

,

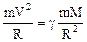или после сокращений:

,

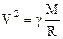откуда скорость для спутника на низкой (R»R₀ – радиус Земли) орбите равна

.

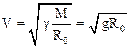Подстановка численных значений дает для первой космической скоростивеличину, равную, приблизительно, 8 км/с.

· Второйкосмическойскоростью называется скорость, которую необходимо сообщить телу, чтобы превратить его в спутник Солнца. В этом случае спутник никогда не возвратится на Землю, т. е. его движение становится инфинитным – неограниченным. Величину скорости находят из закона сохранения энергии: кинетическая энергия спутника у поверхности Земли равна его потенциальной энергии на бесконечно большом расстоянии:

,

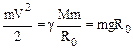подставляя численные значения, получим:

.

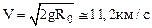· Третьякосмическаяскорость– скорость тела, имея которую оно может покинуть пределы Солнечной системы. Расчеты показывают, что эта скорость, в лучшем случае, составляет около 16,7 км/c. Дело в том, что величена третьей космической скорости зависит от направления запуска спутника. Она меньше, если ракета двигаться в направлении орбитального движения Земли вокруг Солнца (происходит сложение скоростей Земли и ракеты). Бóльшую скорость (~73 км/с) необходимо сообщить, если ракету запускать против движения Земли.