Спектр при угловой модуляции

Лекция №2

Спектры амплитудно-модулированных(АМ) и частотно-модулированных (ЧМ) колебаний

АМ

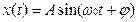сигнал переносчик,

информационный параметр - амплитуда (2.1)

рассмотрим 2 случая:

а) 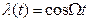- модулирующая функция (гармоника с частотой 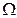) (2.2)

б) 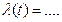(2.3)

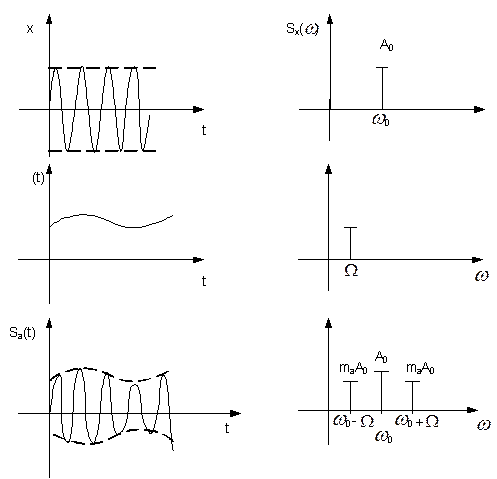
Рис.2.1а Временная область Рис.2.1б Частотная область

1) Изменение амплитуды модулирующей функцией 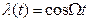, рис.2.1а:

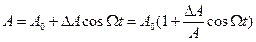(2.4)

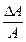= m_a (2.5)

- индекс амплитудной модуляции (относительное изменение амплитуды)

Аналитическое выражение для АМ сигнала для модулирующей функции а)

(2.6)

Разложим 2.6:

S(t) = 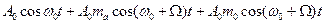(2.7)

- три компоненты с частотами

w₀, w₀+W, w₀-W, спектр - рис.2.1б (2.8)

при W=2pF (2.9)

Ширина спектра:

[Каждая спектральная составляющая в спектре моделируемого сигнала

добавляет в спектр АМ (при амплитудной модуляции) две составляющие]

2) Изменение амплитуды модулирующей функции 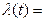…., рис.2.2а :

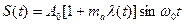(2.10)

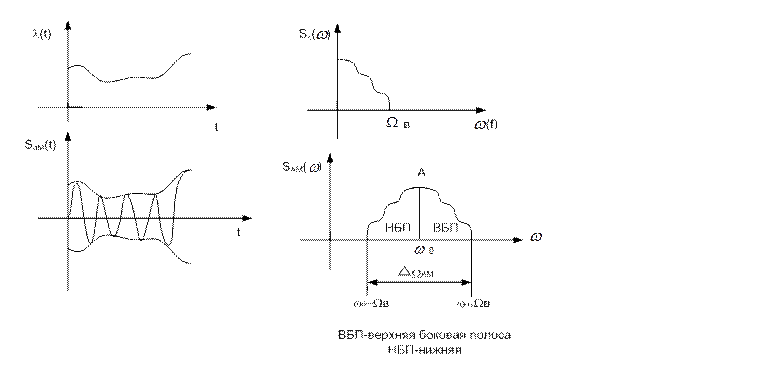рис.2.2а рис.2.2б

Каждая спектральная составляющая в спектре S_l модeлирующего сигнала добавляет в спектр АМ (при амплитудной модуляции) две составляющие.

Wв - верхняя граница спектра низкочастотной модулирующей функции ,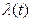

рис.2.2б – спектр модулированного сигнала

[ ширина спектра АМ ] (2.11)

Спектр при угловой модуляции

Угловая модуляция – изменение полного угла (фазы, 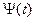) сигнала

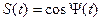(2.12)

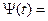
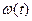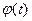+ (2.13)

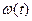- мгновенная частота

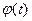- начальная фаза

Можно менять (модулировать) мгновенную частоту – частотная модуляция

или можно менять (модулировать) начальную фазу – фазовая модуляция

Мгновенная частота и полная фаза связаны интегральными соотношениями

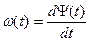(2.14а)

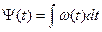(2.14б)

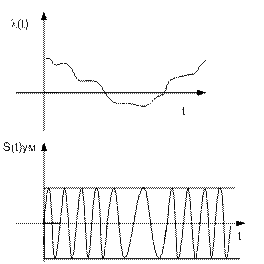
Рис.2.3 Сигнал при угловой модуляции во временной области

Два случая модулирующей функции:

гармоника - а)

и произвольная функция - б)

а)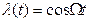

б)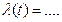

1) воздействуем на начальную фазу- это ФМ:

и (2.15а)

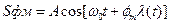(2.15б)

Это аналитические выражения для сигнала с фазовой модуляцией;

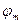- девиация фазы

2) воздействуем на мгновенную частоту, модулирующая функция также а) и б):

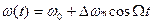(2.16а)

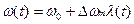(2.16б)

где 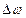m - девиация частоты

Полная фаза при этом

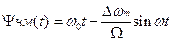, при модулирующей функции а) (2.17а)

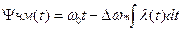, при модулирующей функции б) (2.17б)

Аналитическая запись сигнала с ЧМ, соответственно для модулирующих

функций а) и б):

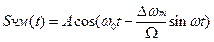(2.18а)

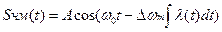(2.18б)

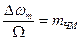- индекс частотной модуляции (2.19)