Строение атома. Квантово-механическая модель атома.

До конца 19 века атом считался неделимым. Затем по мере накопления опытных данных пришлось отказаться от таких взглядов и признать, что атомы имеют сложное строение.

Для объяснения опытных данных по рассеянию 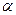- частиц Э. Резерфорд предложил ядерную модель атома. Согласно этой модели атом состоит из массивного положительно заряженного ядра, при этом очень малого по размерам. В ядре сосредоточена почти вся масса атома. Вокруг ядра на значительном расстоянии от него вращаются электроны, образующие электронную оболочку атома.

Размер всего атома составляет около 10^{-8 см, ядра – порядка 10-13 см. По размеру ядро примерно в 100000 раз меньше атома.}

Поскольку атом в целом электронейтрален, то суммарный заряд электронов должен быть равен заряду ядра. Дальнейшие исследования показали, что положительный заряд ядра атома численно равен порядковому номеру элемента в периодической системе Д.И. Менделеева.

Таким образом, число положительных зарядов ядра каждого атома, а также число вращающихся в поле ядра электронов равны порядковому номеру элемента.

Порядковый номер атома титана равен 22. Значит, его положительный заряд равен 22 и в поле ядра вращаются 22 электрона.

При химических реакциях ядро атома не претерпевает изменений. Изменению подвергаются электронные оболочки атомов, строением которых объясняются многие свойства химических элементов. Поэтому состояние электронов в атоме определяет многие свойства.

Электрон – это очень маленькая частица, для которой законы классической механики не выполняются. Такая частица не имеет траектории, обладает волновыми свойствами. Для её характеристики требуется привлечение других понятий. Состояние электронов в атоме описывается квантовой механикой.

Квантовая механика базируется на трех основных положениях:

энергетические изменения, происходящие в микросистемах, носят дискретный характер (принцип квантования энергии);

поведение микрочастиц (в том числе и электронов) определяется двойственностью их природы (корпускулярно-волновой дуализм);

законы микромира обусловлены статистическим (вероятностным) характером.

Квантование энергии. Для объяснения способностей излучения нагретых тел М. Планк в 1900 г. выдвинул предположение, что энергия излучается и поглощается не непрерывно, а дискретно отдельными порциями – квантами. Энергия Е кванта зависит от частоты электромагнитного излучения ν:

Е=hν (1),

где h – постоянная Планка; ν=с/λ (λ – длина волны излучения); с – скорость света. Идея о квантовании энергии позволила объяснить фотоэлектрический эффект (А.Эйнштейн,1905) и линейчатую структуру атомных спектров (Н. Бор,1913).

Корпускулярно-волновой дуализм характеризует способность любого объекта проявлять одновременно волновые и материальные свойства. Двойственная природа микромира была впервые установлена для излучения. С одной стороны, для излучения характерны такие явления, как интерференция и дифракция, которые характеризуют его волновую природу. С другой стороны, излучение проявляет свойства частиц, о чем свидетельствует явление фотоэффекта. Эйнштейн предположил, что излучение испускается в виде частиц, называемых фотонами или квантами. Каждый фотон обладает энергией, определяемой (1).

В силу корпускулярной природы излучения фотоны должны обладать определенной массой. Масса покоя фотона равна нулю, а при движении фотон приобретает динамическую массу. Для вычисления этой массы Эйнштейн обосновал применение уравнение эквивалентности массы и энергии:

Е=mc².

В то же время Е=hν=h(с/λ). Отсюда следует

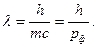(2).

Здесь р_ф=mc – импульс фотона. Французский физик Л. де Бройль в 1923 г. предположил, что двойственной природой обладает не только свет, но и любой материальный объект (в частности, электрон). Длина волны любого движущегося объекта

(3),

где m – масса частицы; 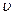- скорость движения частицы; λ – длина волны объекта, называемая длиной волны де Бройля. Из этого выражения следует, что чем меньше масса частицы, тем больше длина ее волны и тем значительней проявляются ее волновые свойства.

Уравнение де Бройля (3) в 1927 г. было подтверждено экспериментально. Американские физики Дж. Дэвиссон и А. Джермер обнаружили дифракцию электронов на монокристаллах никеля Ni. Позднее способность к дифракции была обнаружена у других микрообъемов (атомов гелия Не, молекул водорода Н₂, нейтронов).

В макромире волновые свойства не проявляются – перемещение тел хорошо описывается как движение частиц. Причина заключается в том, что постоянная Планка очень мала, поэтому длины волн оказываются соизмеримыми с размерами частиц только в микромире.

Принцип неопределенности. Волновые свойства микрочастиц выражаются также в ограниченности применения к ним некоторых понятий классической механики, а именно координаты и импульса. Например, один из способов наблюдения за объектом – воздействие на него электромагнитного излучения (свет, радиоволны) и регистрация отраженного сигнала, что широко используется в радиолокации, эхолокации. Причем чем сильнее воздействие на наблюдаемый объект, тем сильнее отраженный сигнал. Если ведется наблюдение за микрообъектами, то действие на них электромагнитного излучения не изменяет ни их положения, ни их скорости. В случае наблюдения за объектами микромира (например, электронами) ситуация выглядит иначе. При действии кванта света (фотона) на микрочастицу ее скорость не остается без изменения. Зная положение микрочастицы в какой-то момент времени, нельзя в это же мгновение определить ее скорость, поскольку она уже изменилась.

В. Гейзенберг в 1927 г. предложил соотношения, которые получили название принципа неопределенности. Согласно этому принципу, невозможно одновременно точно определить координаты частица и ее импульс.

Математически принцип неопределенности формулируется следующим образом:

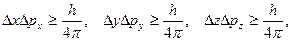
где Δx, Δy, Δz – погрешность определения координат x, y, z соответственно; Δp_x, Δp_y, Δp_z – погрешность определения проекций импульса на оси координат. Из этих соотношений следует, что чем точнее определены координаты электрона, тем с меньшей точностью будет найден его импульс, и наоборот. Другими словами, говорить о траектории движения электрона не имеет смысла, так как для ее описания необходимо точно знать координаты электрона и его импульс в каждый момент времени. Из соотношений неопределенности следует, что точно описать движение такой микрочастицы, как электрон невозможно. Движение электрона можно описать, используя вероятностный подход, причем есть лишь определенная вероятность нахождения электрона в заданной области пространства.

Движущейся частице можно поставить в соответствие волновой процесс с длиной волны (3), тогда этот процесс будет характеризоваться частотой ν и волновой функцией Ψ – величиной, определяющей волнообразно распространяющееся возмущение.

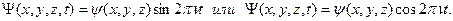
Здесь ψ(x, y, z) – амплитуда волн де Бройля или координатная волновая функция, зависящая только от пространственных координат.

Стационарное уравнение Шрёдингера.

Законы движения частиц в квантовой механике выражаютсяуравнением Шрёдингера, которое играет ту же роль, что и законы Ньютона в классической механике. Уравнение Шрёдингера представляет собой дифференциальное уравнение в частных производных. Э. Шрёдингер в 1926 г. предложил использовать волновое уравнение в качестве модели для описания поведения электрона в атоме – уравнение, связывающее энергию системы с ее волновым движением. Стационарное уравнение Шрёдингера для одной части можно записать в следующей форме:

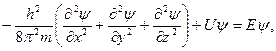(4)

где U – потенциальная энергия частицы; Е – ее полная энергия; x, y, z – декартовы координаты. Входящую в (4) переменную величину называют ψ волновой функцией. Эта функция описывает все свойства системы в стационарном состоянии – состоянии, которое не изменяется во времени. Функция ψ зависит от координат частиц и может зависеть от времени. Квадрат ее абсолютной величины |ψ|² характеризует вероятность нахождения частицы в данном месте пространства. Величина |ψ|²dV равна вероятности нахождения рассматриваемой частицы в элементе объема dV=dxdydz.

Уравнение Шрёдингера часто записывают в следующей форме:

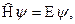(5)

где 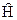- оператор Гамильтона:

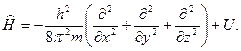(6)

Квантово-механическое решение задач в теории атома и молекулы сводится к нахождению удовлетворяющих уравнению Шрёдингера волновых функций и значений энергии. Вообще говоря, может быть несколько различных функций ψ₁, ψ₂, ψ₃, …, ψ_n, которые являются решениями уравнения Шрёдингера, причем каждой соответствует свое значение энергии E₁, E₂, …, E_n.

Волновые функции, для которых уравнение Шрёдингера имеет решение, называют собственными функциями; значения энергии, вычисленные из таких решений – собственными значениями.

Таким образом, согласно представлениям квантовой механики, вероятность пребывания электрона в различных областях пространства неодинакова. Современным представлениям отвечает понятие об электронном облаке, плотность которого в различных точках определяется |ψ|². В научной литературе используют понятие «орбиталь», которое характеризует совокупность положений электрона в атоме. Каждой орбитали соответствует определенная волновая функция.

Уравнение (6) в сферических координатах приобретает вид

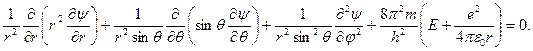
Решая это уравнение, получают

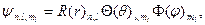(7)

где R(r) – радикальная составляющая волновой функции; Θ(θ) и Φ(φ) – угловые составляющие волновой функции. Следовательно, волновые функции в (7) зависят от трех целочисленных параметров n, l и m, которые называют квантовыми числами.