Вынужденные колебания. Резонанс. Все рассмотренные нами ранее колебания называются свободными или собственными
Все рассмотренные нами ранее колебания называются свободными или собственными. Выведенная из положения равновесия или получившая начальный импульс система совершает колебания, будучи предоставлена самой себе.
Рассмотрим теперь материальную точку, на которую кроме упругой силы и силы трения действует периодическая сила, изменяющаяся по гармоническому закону
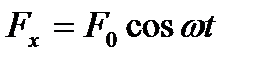 . (11)
. (11)
Тогда дифференциальное уравнение движения будет иметь вид
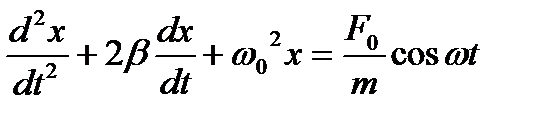 . (12)
. (12)
 Рассмотрим движение, описываемое этим уравнением, исходя из общих физических представлений. Пусть в начальный момент времени материальная точка покоилась, находясь в положении равновесия. Включение периодической силы (11) приведёт к раскачиванию материальной точки. Работа этой силы будет идти на сообщение кинетической энергии материальной точке и на преодоление силы сопротивления. Сила сопротивления пропорциональна скорости материальной точки.
Рассмотрим движение, описываемое этим уравнением, исходя из общих физических представлений. Пусть в начальный момент времени материальная точка покоилась, находясь в положении равновесия. Включение периодической силы (11) приведёт к раскачиванию материальной точки. Работа этой силы будет идти на сообщение кинетической энергии материальной точке и на преодоление силы сопротивления. Сила сопротивления пропорциональна скорости материальной точки.
Поэтому увеличение кинетической энергии возможно только до некоторого предела. После этого наступает динамическое равновесие, когда работа внешней силы полностью расходуется на преодоление сопротивления, а амплитуда колебаний остаётся постоянной. Начальному отрезку времени, когда наблюдается постепенное возрастание амплитуды колебаний, соответствует переходный режим колебаний. Далее, когда амплитуда колебаний перестаёт возрастать, наступает стационарный режим колебаний. Стационарный режим колебаний представляет собой гармоническое колебание с частотой, равной частоте вынуждающей силы 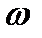 . Но благодаря инерции колебания материальной точки будут отставать по фазе от колебаний внешней периодической силы
. Но благодаря инерции колебания материальной точки будут отставать по фазе от колебаний внешней периодической силы
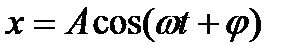 . (13)
. (13)
Колебания материальной точки под действием внешней периодической силы, описываемые уравнением (12) называют вынужденными колебаниями. Амплитуда колебаний А и сдвиг фаз 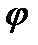 определяются параметрами колеблющейся системы. Найдём А и
определяются параметрами колеблющейся системы. Найдём А и 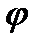 . Для этого:
. Для этого:
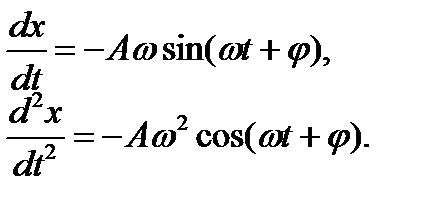 (14)
(14)
После подстановки (14) в (12) и преобразования правой части:
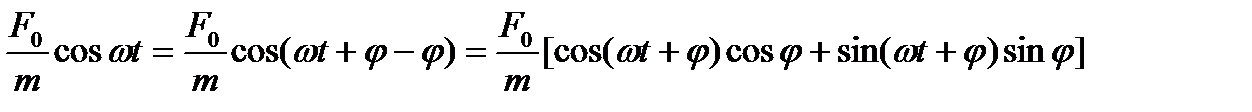 .(15)
.(15)
Получаем:
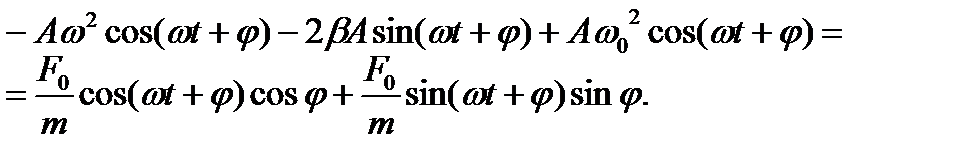 (16)
(16)
Это тождество может выполняться только при условии, что коэффициенты при одинаковых функциях левой и правой частей тождества равны:
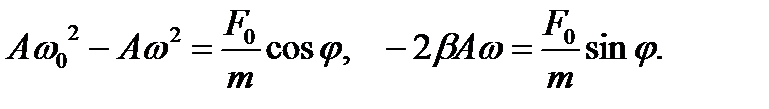 (17)
(17)
Эта система уравнений позволяет найти:
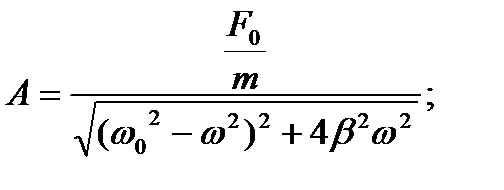
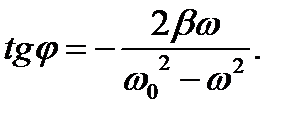 (18)
(18)
Полученные выражения показывают, что величина амплитуды вынужденных колебаний А зависит от амплитуды вынуждающей силы 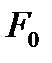 , собственной частоты
, собственной частоты 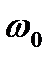 и частоты
и частоты 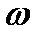 , а также от коэффициента затухания
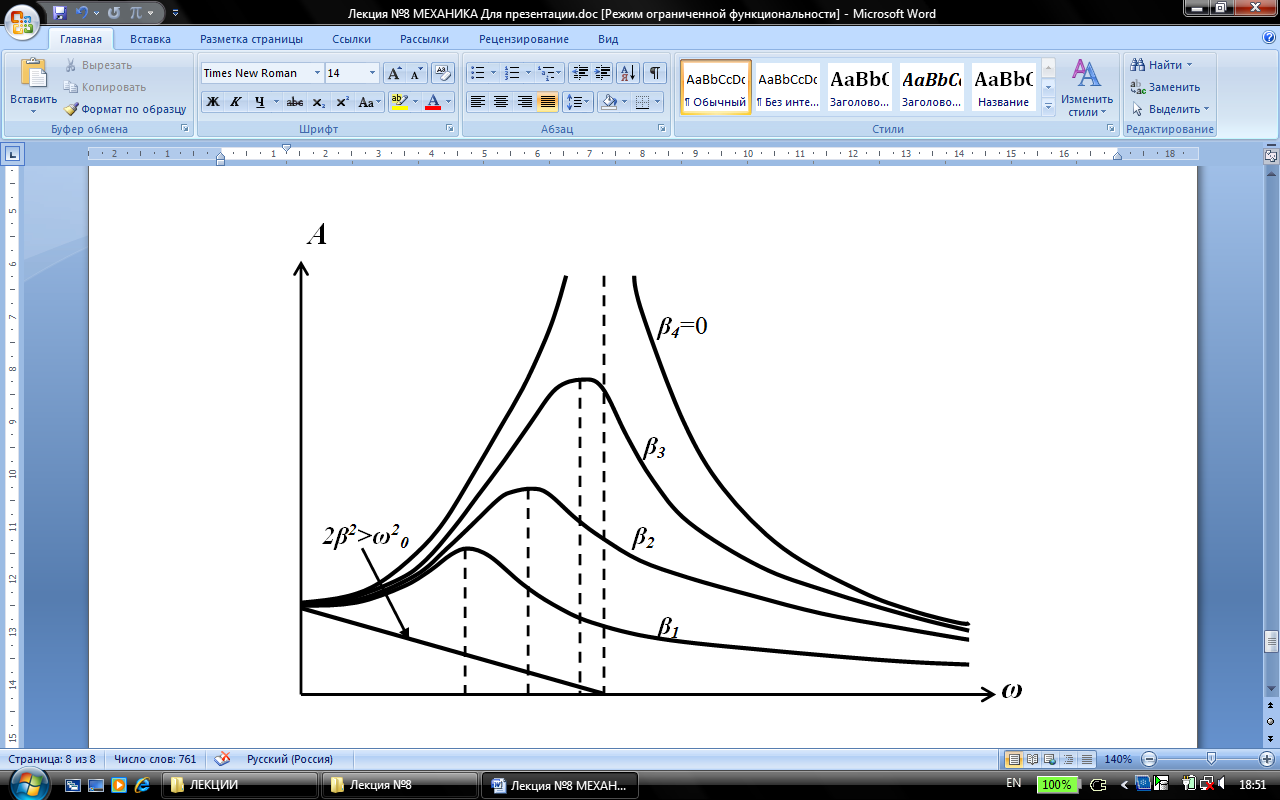
, а также от коэффициента затухания 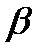 . Зависимость амплитуды от частоты вынуждающей силы приводит к тому, что при некоторой определённой для данной системы частоте амплитуда достигает максимального значения. Это явление называется резонансом, а соответствующая частота – резонансной.
. Зависимость амплитуды от частоты вынуждающей силы приводит к тому, что при некоторой определённой для данной системы частоте амплитуда достигает максимального значения. Это явление называется резонансом, а соответствующая частота – резонансной.
При резонансной частоте колебательная система оказывается наиболее отзывчивой на действие вынуждающей силы. Для нахождения резонансной частоты нужно найти максимум функции 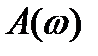 . Или, что тоже самое, минимум в знаменателе в выражении для А (18). Для этого продифференцируем подкоренное выражение по
. Или, что тоже самое, минимум в знаменателе в выражении для А (18). Для этого продифференцируем подкоренное выражение по 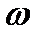 и приравняем его к нулю:
и приравняем его к нулю:
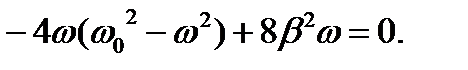
 Корни:
Корни:
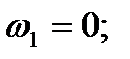
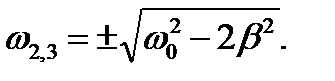
Отбросив два корня (нулевой и отрицательный), получаем требуемое выражение для резонансной частоты:
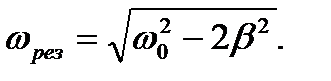
Подставим его в выражение (18) и получим формулу для вычисления величины амплитуды при резонансе:
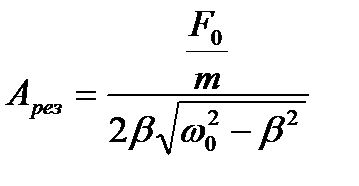 .
.
Отсюда видно, что если коэффициент затухания стремиться к нулю 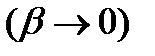 , то резонансная частота стремиться к величине
, то резонансная частота стремиться к величине 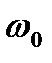
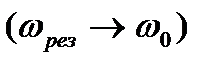 , а резонансная амплитуда стремиться к бесконечности.
, а резонансная амплитуда стремиться к бесконечности.
Зависимость амплитуды от частоты при заданном коэффициенте затухания называется резонансной кривой.
Сложение гармонических колебаний одного направления и одинаковой частоты
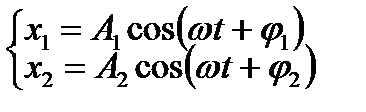

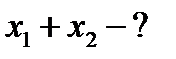
Используется метод векторных диаграмм:
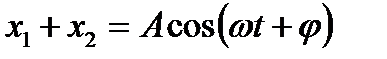
 ;
;
По теореме косинусов
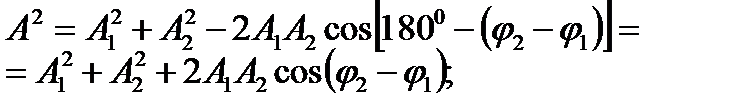
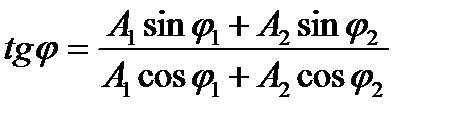 .
.
1) Если 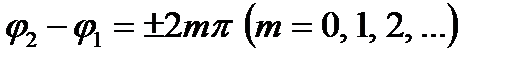 ,
,
то 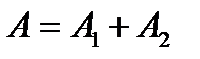 .
.
2) Если 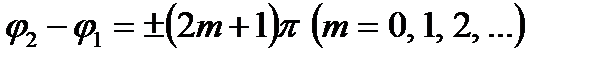 ,
,
то 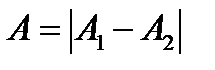 .
.
Сложение взаимно перпендикулярных гармонических колебаний
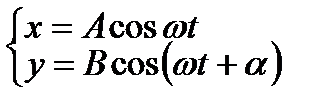

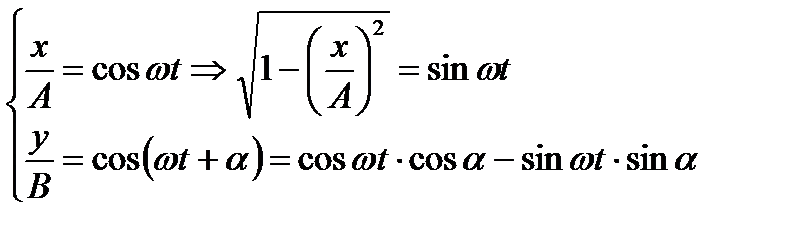
После подстановки выражений для 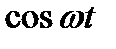 и
и 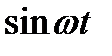 в последнее уравнение:
в последнее уравнение:
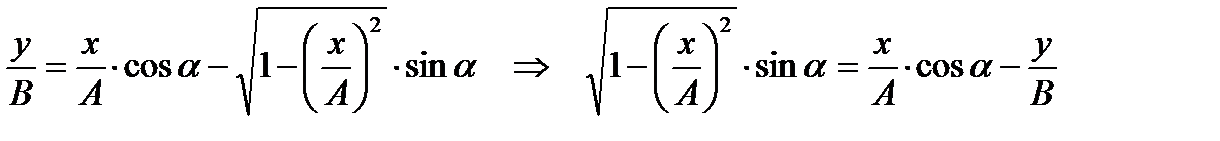 ;
;
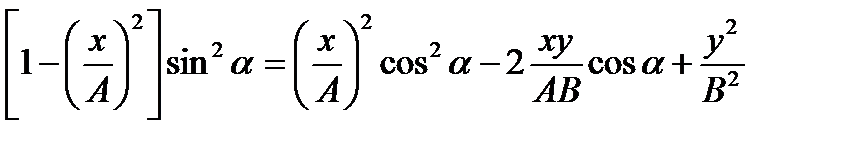 ;
;
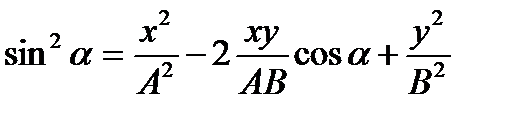 ;
;
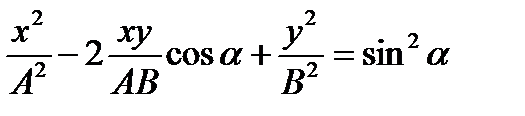 – уравнение эллипса, в случае, когда оси эллипса произвольно ориентированы относительно декартовых осей координат.
– уравнение эллипса, в случае, когда оси эллипса произвольно ориентированы относительно декартовых осей координат.
1. Если α=mπ (m=0, ±1, ±2, …), то sinα=0, cosα=±1 и эллипс вырождается в прямую:
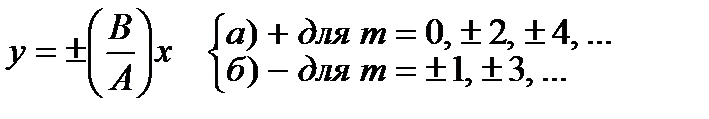
Амплитуда 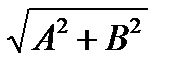 ;
; 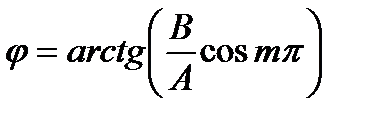
m = 0, ±2, ±4, … m = ±1, ±3, …
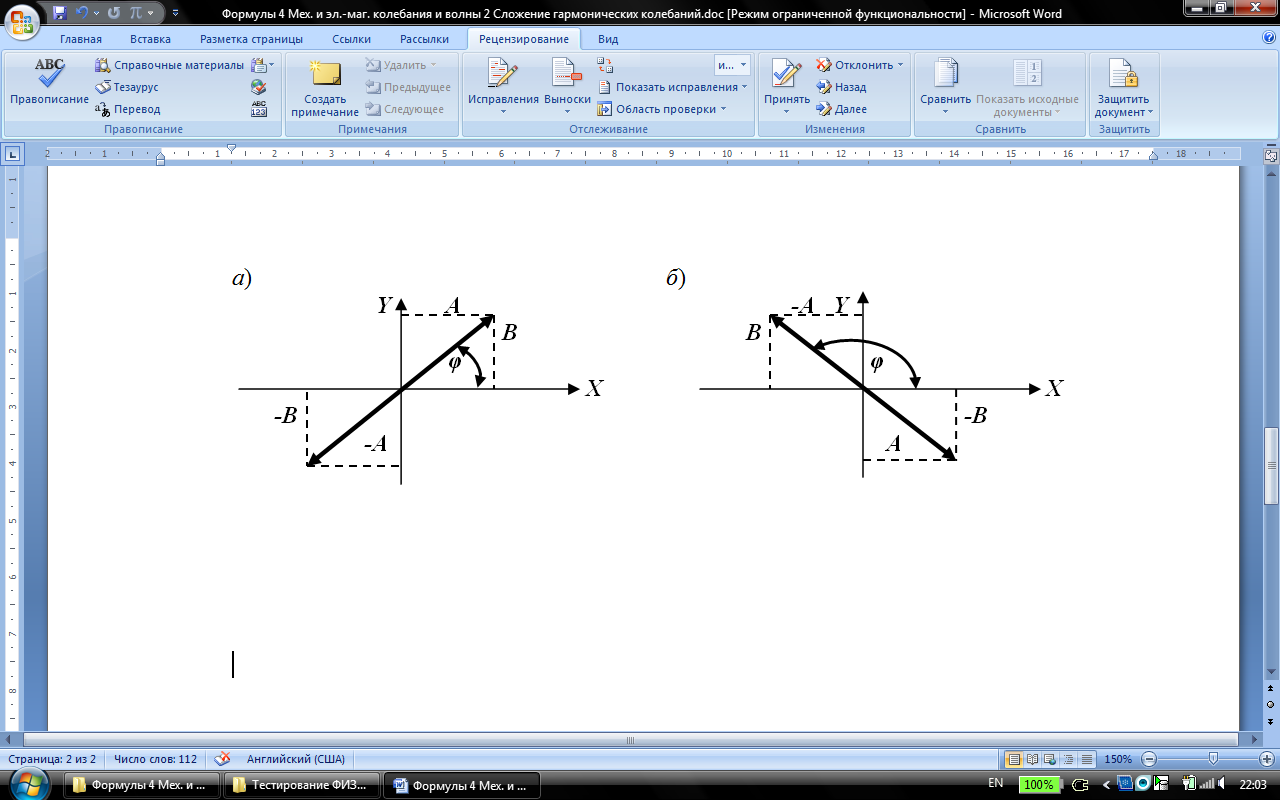
 2. Если
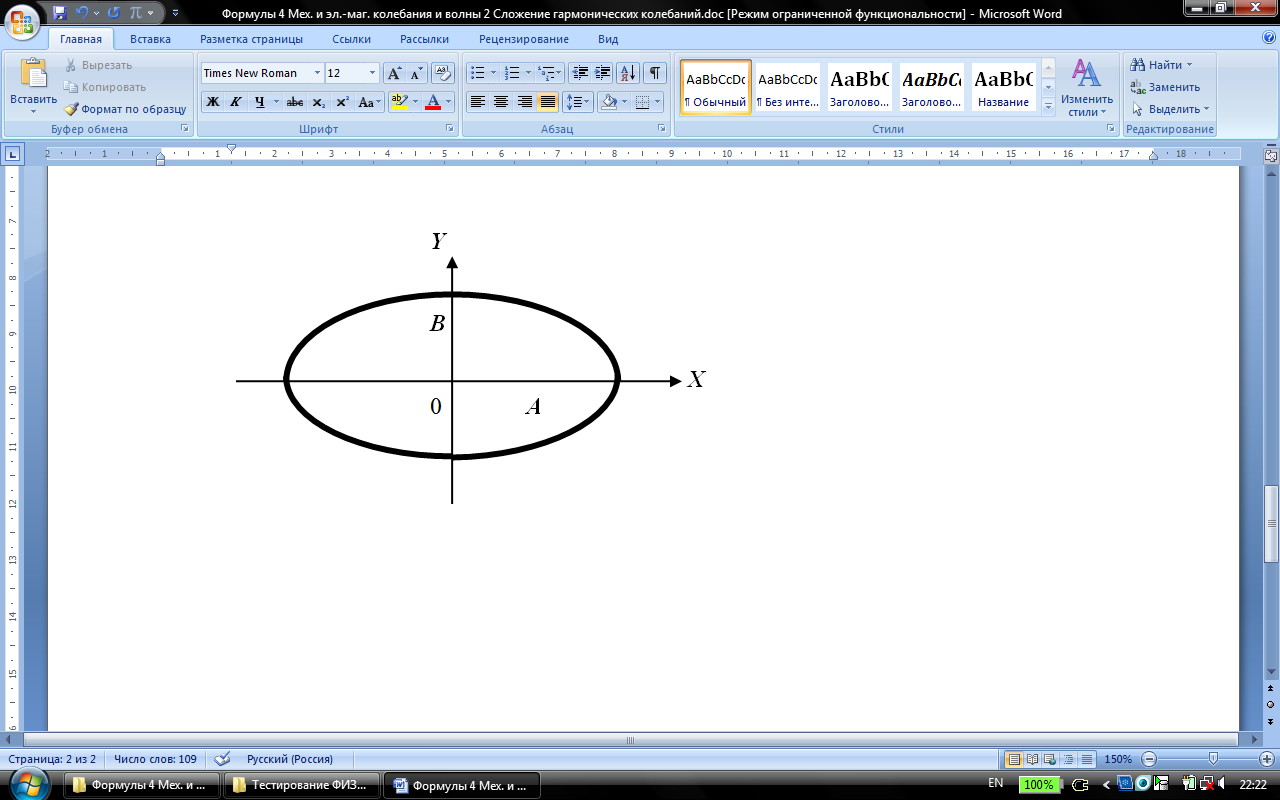
2. Если 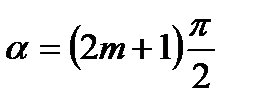 , то cosα=0, sin2α=1.
, то cosα=0, sin2α=1.
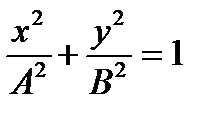 – уравнение эллипса.
– уравнение эллипса.
Для соотношений частот – отношение частот складываемых колебаний равно отношению числа пересечений фигур Лиссажу с прямыми, параллельными осям координат:
при соотношении частот 1:1
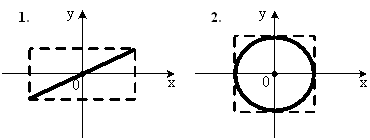
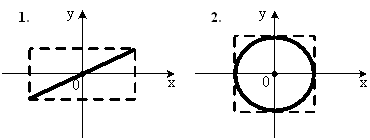
при соотношении частот 2:1
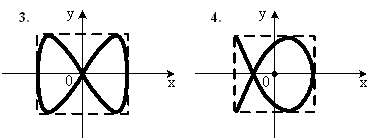
при соотношении частот 3:2
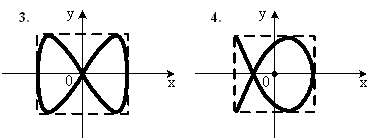
Дата добавления: 2015-08-08; просмотров: 954;
