Вынужденные колебания. Рассмотрим колебания материальной точки при наличии периодической внешней силы

Рассмотрим колебания материальной точки при наличии периодической внешней силы

,

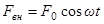действующей вдоль оси 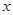. Уравнение движения в этом случае принимает вид:

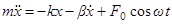, или в приведенном виде

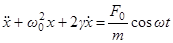. (2)

Уравнение (2) называется неоднородным дифференциальным уравнением 2 – го порядка, а уравнение (1) соответствующим ему однородным уравнением.

В теории дифференциальных уравнений доказывается следующая теорема.

Общее решение неоднородного дифференциального уравнения равно сумме общего решения однородного уравнения и частного решения неоднородного уравнения.

Общее решение однородного уравнения:

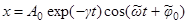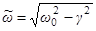, где . (3)

Частное решение неоднородного уравнения будем искать в виде:

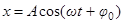. (4)

Следует отметить, что амплитуда 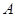и фаза 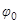в этом решении уже не определяются лишь начальными условиями как в свободных колебаниях, а зависят от параметров колебательной системы. Подставляя решение (4) в уравнение (2), можно получить следующие выражения для 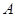и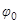

, .

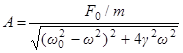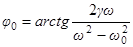Общее решение уравнения (2) является суммой решений (3) и (4). При 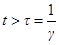решение (3) станет пренебрежимо малым и установятся вынужденные колебания вида (4). По этой причине величина 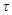называется временем установления колебаний.

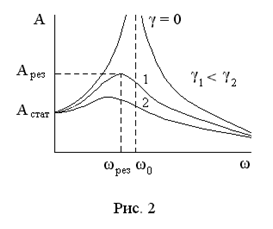На рис. 2 приведена зависимость амплитуды вынужденных колебаний 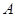от частоты вынуждающей силы 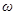. Амплитуда имеет максимальное значение при

.

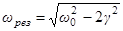Это явление резонанса вынужденных колеба-ний. С ростом коэффициента затухания 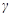резонансная частота 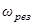и резонансная амплитуда 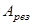уменьшаются. В отсутствие затухания ( 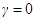) 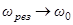и 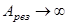. Физически это происходит из-за того, что в колебательную систему непрерывно поступает энергия за счет работы внешней силы, а потери энергии отсутствуют.

При 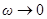амплитуда 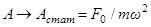. Величина 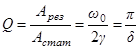называется добротностью колебательной системы.