Перевод чисел из различных систем счисления

Перевод чисел из любой системы счисления в десятичную легко осуществить сложением произведений цифр этих чисел на их вес в данной системе счисления 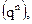например:

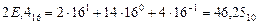
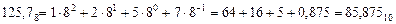
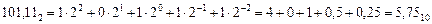
Пример тестового задания. Даны десятичное число 100 и двоичное число 110₂. Найти их произведение в десятичной системе. Варианты правильных ответов: 88; 600; 24; 11000.

Перевод целых чисел из десятичной системы счисления в двоичнуюрассмотрим на примере:

Пример №1:

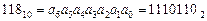
Исходное число / 2	Частное (целая часть)	Остаток от деления	Разряд двоичного числа
118/2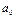
59/2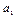
29/2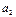
14/2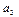
7/2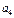
3/2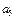
1/2	–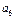

Пример №2:

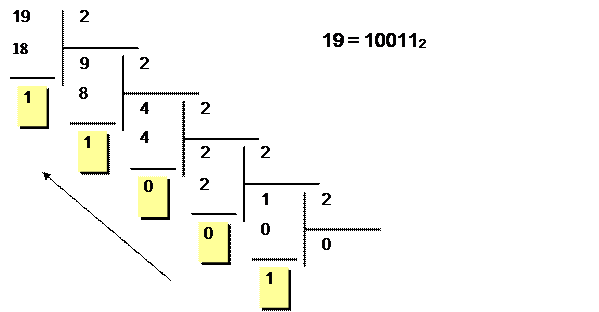Пример №3:

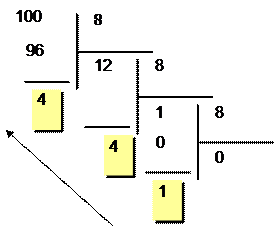100= 144₈

Задача № 1 : Последняя цифра числа 78965431267₁₀ в двоичной системе счисления равна ….?

Решение: Последняя цифра числа в двоичной системе соответствует младшему разряду двоичного числа, т.е. первому остатку от деления исходного десятичного числа на базис 2. Так как 7 –нечетное число, то остаток равен 1.

Перевод правильной десятичной дроби в двоичную системуосуществляется следующим образом : умножить переводимое число на основание новой системы, далее от результата отделить целую часть, а оставшуюся дробную часть снова умножить на это основание. Процесс такого умножения повторяется до получения нулевого результата. Полученная дробная часть справа от запятой записывается как целые части произведений в порядке их получения.

В качестве примера рассмотрим перевод правильной десятичной дроби 0,625.

1) 1 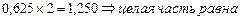старший разряд числа справа от запятой

2) 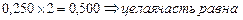0 ( целую часть отбрасываем)

3) 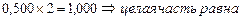1

4) 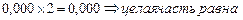0 младший разряд числа справа от запятой

Результат: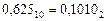

Перевод смешанного десятичного числа в двоичную систему:отдельно переводятся целая и дробная часть (правильная десятичная дробь), а в записи результата целая часть перевода отделяется от дробной части запятой.

Например: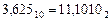

Здесь целая часть 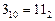, а дробная часть 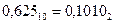(смотри пример выше)

Задача № 2:Перевести 45,75₁₀ в двоичную систему счисления.

Решение:

1) Отдельно переводим целую часть, т.е. число 45=101101₂

Исходное число / 2	Частное (целая часть)	Остаток от деления	Разряд двоичного числа
45/2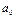
22/2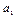
11/2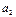
5/2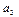
2/2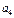
1/2	-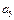

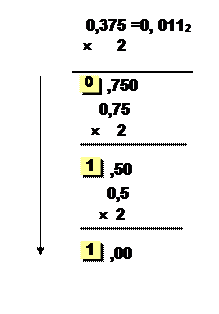
2) Отдельно переводим дробную часть числа (справа от запятой), т.е. 0,75 в двоичный код:

1) 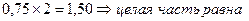1 старший разряд (целую часть отбрасываем)

2) 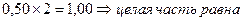1 здесь вновь целую часть отбрасываем

3) 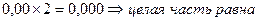0 младший разряд числа справа от запятой

Результат: 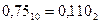Итого: 45,75₁₀ = 101101, 110₂

Пример №2:

 

Перевод целых чисел из десятичной системы счисления в пятеричнуюрассмотрим на примере:

 

2009₁₀ =31014₅

 

Исходное число / 5	Частное (целая часть)	Остаток от деления	Разряд двоичного числа
2009/5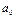
401/5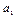
80/5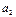
16/5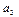
	-

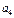
Перевод целых чисел из десятичной системы счисления в восьмеричнуюрассмотрим на примере: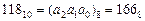

Исходное число / 8	Частное (целая часть)	Остаток от деления	Разряд двоичного числа
118/8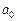
14/8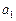
1/8	–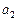

Перевод восьмеричных чисел в двоичныевыполняется записью каждой цифры исходного восьмеричного числа тремя цифрами (триадами) в двоичном коде, например:

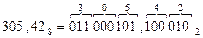
Перевод шестнадцатеричных чисел в двоичные осуществляется записью каждой цифры исходного шестнадцатеричного числа четырьмя двоичными числами (тетрадами), например:

;

 

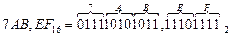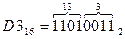
Перевод двоичных чисел в восьмеричные:

Вправо и влево от запятой исходное число разбивается на триады, недостающие крайние цифры заменяются нулями. Выделенные двоичные триады заменяются восьмеричными цифрами, например:

 

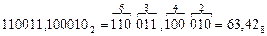
Перевод двоичных чисел в шестнадцатеричные:

Вправо и влево от запятой исходное число разбивается на тетрады, недостающие крайние цифры заменяются нулями. Выделенные двоичные тетрады заменяются шестнадцатеричными цифрами. Пример:

 

 

123

---

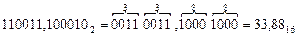
Дата добавления: 2015-08-08; просмотров: 1209;

---