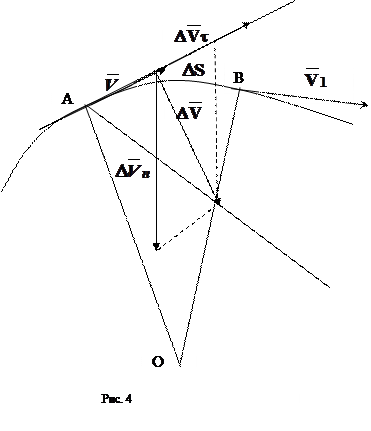
Ускорение и его составляющие. Рассмотрим плоское движение (рис

Рассмотрим плоское движение (рис. 4).

Перенесем вектор 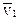в точку А и найдем .

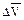Среднее ускорение . (1.7)

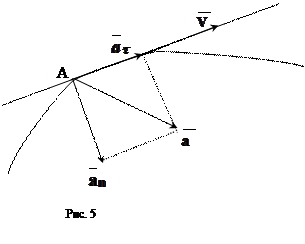
Мгновенное ускорение 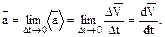(1.8)

Мгновенное ускорение равно первой производной скорости по времени.

Разложим вектор 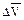на две составляющие: и .

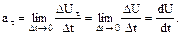(1.9)

Нормальная составляющая ускорения характеризует быстроту изменения скорости по направлению и направлена к центру кривизны траектории (рис. 5).

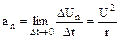. (1.10)

Полное ускорение есть геометрическая сумма тангенциальной и нормальной составляющих:

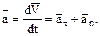(1.11)

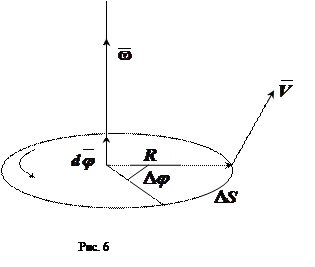
Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени, направление которой соответствует правилу правого винта (рис. 6):

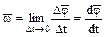. (1.12)

Линейная скорость точки 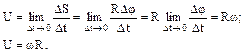(1.13)

Или в векторном виде 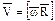. (1.14)

Время, за которое точка совершает один полный оборот, называется периодом вращения: 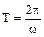. (1.15)

Число полных оборотов, совершаемых телом в единицу времени, называется частотой вращения:

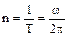, (1.16)

откуда

ω = 2 π n. (1.17)

Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени:

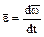. (1.18)

Тангенциальная составляющая ускорения 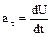, (1.19)

где U = ωR.

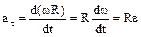. (1.20)

Нормальная составляющая ускорения 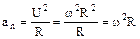. (1.21)