Расчетный метод оценки коэффициента чувствительности к асимметрии цикла напряжений с учетом их концентрации
Выше был рассмотрен метод оценки коэффициента чувствительности детали к асимметрии цикла нагружения с учетом комплекса конструкционных и технологических факторов. Однако, широкого теоретического или экспериментального обоснования этот метод не получил, хотя и нашел применение на практике.
В настоящем разделе с учетом материала, изложенного в п.2.13, дается теоретическое обоснование оценки влияния концентрации напряжений на уровень коэффициента чувствительности детали к асимметрии нагружения для рассмотренных выше подходов к построению диаграммы предельных амплитуд при наличии концентрации напряжений.
В соответствии с формулой (2.104) при отсутствии других факторов, влияющих на величину К, коэффициент чувствительности к асимметрии цикла нагружения при наличии концентратора напряжений определяется соотношением
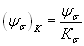 . (2.116)
. (2.116)
Опытные данные, заимствованные из ряда литературных источников различных авторов и представленные на рис. 2.22, и результаты проведенных корреляционного и регрессионного анализов [4] указывают на отсутствие зависимости, представленной формулой (2.116). Так, например, коэффициент корреляции между случайными величинами  и
и 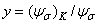 оказался незначимо отличающимся от нуля (r = -0.066 при
оказался незначимо отличающимся от нуля (r = -0.066 при 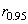 =0,457). Поэтому линия регрессии 1на рис. 2.22 почти горизонтальна. Более того, она проходит заметно выше линии с ординатами точек, равных единице, что говорит о более высокой чувствительности материала к асимметрии цикла при наличии концентрации напряжений в образцах. Обращает на себя внимание значительный разброс экспериментальных данных вокруг линии регрессии. Мера индивидуального рассеяния составляет
=0,457). Поэтому линия регрессии 1на рис. 2.22 почти горизонтальна. Более того, она проходит заметно выше линии с ординатами точек, равных единице, что говорит о более высокой чувствительности материала к асимметрии цикла при наличии концентрации напряжений в образцах. Обращает на себя внимание значительный разброс экспериментальных данных вокруг линии регрессии. Мера индивидуального рассеяния составляет 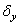 =0.43.
=0.43.
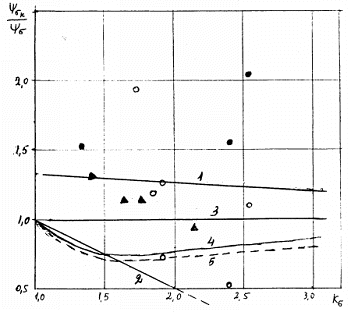
Рис. 2.22. Величины отношения  для различных значений коэффициента концентрации напряжений
для различных значений коэффициента концентрации напряжений 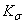 :
:
Точки — эксперимент: 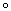 — алюминиевые сплавы,
— алюминиевые сплавы,  — титановые сплавы,
— титановые сплавы,  — стали;
— стали;
Линии — расчет: 1 — на базе регрессионного анализа,
2 — по формуле (2.119),
3 — по методике К.Ганна,
4 — по методике Р.Хэйвуда для алюминиевых сплавов,
5 — по методике Р.Хэйвуда для сталей.
При использовании для построения диаграммы предельных амплитуд метода С.В.Серенсена, Р.С.Киносошвили и В.П.Когаева уравнение диаграммы с учетом концентрации напряжений в соответствии с (2.3) и (2.33) будет иметь вид
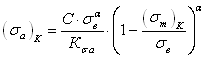 . (2.117)
. (2.117)
В этом случае коэффициент чувствительности к асимметрии цикла напряжений
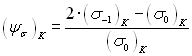 , (2.118)
, (2.118)
где  и
и 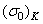 — пределы выносливости образцов с концентраторами напряжений при симметричном и отнулевом циклах соответственно, вычисляют методом последовательных приближений из уравнения
— пределы выносливости образцов с концентраторами напряжений при симметричном и отнулевом циклах соответственно, вычисляют методом последовательных приближений из уравнения
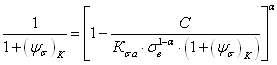 . (2.119)
. (2.119)
Для всех рассмотренных конструкционных материалов (алюминиевые и титановые сплавы, стали) величина 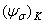 , найденная из уравнения (2.119), примерно в
, найденная из уравнения (2.119), примерно в 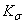 раз ниже соответствующей характеристики для гладких образцов, причем, коэффициент
раз ниже соответствующей характеристики для гладких образцов, причем, коэффициент 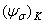 монотонно убывает с ростом предела прочности материала.
монотонно убывает с ростом предела прочности материала.
Сопоставление расчетных значений 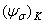 и результатов экспериментов для алюминиевых сплавов показало, что рассмотренный метод дает значительное (от 2 до 5 раз) занижение коэффициента чувствительности к асимметрии цикла нагружения по сравнению с опытными данными. Аналогичные результаты следует ожидать и для других конструкционных материалов. На рис.2.22 расчетные данные по формуле (2.119) показаны линией 2.
и результатов экспериментов для алюминиевых сплавов показало, что рассмотренный метод дает значительное (от 2 до 5 раз) занижение коэффициента чувствительности к асимметрии цикла нагружения по сравнению с опытными данными. Аналогичные результаты следует ожидать и для других конструкционных материалов. На рис.2.22 расчетные данные по формуле (2.119) показаны линией 2.
В связи с этим соответствующие рекомендации действующего стандарта должны быть подвергнуты корректировке.
Использование метода К. Ганна для построения диаграммы предельных амплитуд цикла нагружения при наличии концентрации напряжений в пределах упругих деформаций, что имеет место при предельном отнулевом цикле, приводит к следующему уравнению диаграммы:
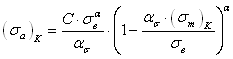 . (2.120)
. (2.120)
Коэффициент чувствительности к асимметрии цикла образца с концентратором напряжений 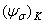 с учетом (2.120) вычисляют с помощью уравнения
с учетом (2.120) вычисляют с помощью уравнения
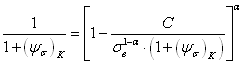 , (2.121)
, (2.121)
которое в точности совпадает с уравнением (2.75), соответствующим гладким лабораторным образцам. Таким образом, из метода К.Ганна следует вывод о равенстве коэффициентов чувствительности к асимметрии цикла напряжений гладких и надрезанных образцов, то есть 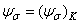 , что так же не согласуется с имеющимися опытными данными. На рис.2.22 расчетные данные по формуле (2.121) представлены линией 3.
, что так же не согласуется с имеющимися опытными данными. На рис.2.22 расчетные данные по формуле (2.121) представлены линией 3.
Рассмотренный ранее метод Р. Хэйвуда для построения диаграммы предельных амплитуд цикла напряжений при наличии концентратора напряжений определяет следующий вид уравнения диаграммы:
 , (2.122)
, (2.122)
которое приводит к уравнению для вычисления коэффициента чувствительности к асимметрии цикла напряжений в виде
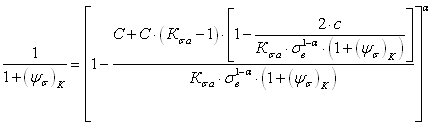 (2.123)
(2.123)
В качестве примера в таблице 2.12 приведены результаты расчетов по формуле (2.123) значений 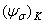 для сталей различной прочности и величины эффектного коэффициента концентрации напряжений
для сталей различной прочности и величины эффектного коэффициента концентрации напряжений 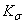 .
.
Таблица 2.12. Значения коэффициента чувствительности к асимметрии цикла напряжений 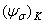 для сталей, вычисленные по уравнению (2.123).
для сталей, вычисленные по уравнению (2.123).
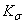
| 1,0 | 1,1 | 1,3 | 1,5 | 2,0 | 3,0 | 4,0 |
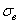 , МПа , МПа
| |||||||
| 0,489 | 0,447 | 0,389 | 0,354 | 0,319 | 0,325 | 0,346 | |
| 0,430 | 0,395 | 0,347 | 0,319 | 0,292 | 0,298 | 0,316 | |
| 0,399 | 0.367 | 0,324 | 0,300 | 0,277 | 0,283 | 0,298 | |
| 0,379 | 0,349 | 0,309 | 0,287 | 0,266 | 0,272 | 0,287 | |
| 0,363 | 0,335 | 0,298 | 0,277 | 0,258 | 0,264 | 0,278 | |
| 0,351 | 0,325 | 0,289 | 0,270 | 0,252 | 0,258 | 0,271 | |
| 0,341 | 0,316 | 0,282 | 0,263 | 0,247 | 0,252 | 0,265 |
Как следует из приведенных данных, поведение коэффициента 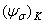 с изменением
с изменением 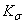 не однозначно. Так, например, для сталей с
не однозначно. Так, например, для сталей с 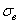 =1200 МПа при увеличении
=1200 МПа при увеличении 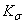 от 1,0 до 2,0 значение
от 1,0 до 2,0 значение 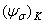 убывает с 0,379 до 0,266, то есть в 1.42 раза. При
убывает с 0,379 до 0,266, то есть в 1.42 раза. При 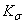 =2 снижение
=2 снижение 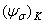 прекращается, а при дальнейшем увеличении
прекращается, а при дальнейшем увеличении 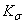 до 4,0 коэффициент
до 4,0 коэффициент 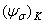 возрастает до величины 0,287. Таким образом, при
возрастает до величины 0,287. Таким образом, при 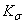 =4 снижение
=4 снижение 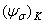 в соответствии с уравнением (2.123) составляет лишь 1.32 раза. На рис. 2.22 расчетные данные по формуле (2.123) представлены линиями 4 и 5 для алюминиевых сплавов и сталей соответственно. Этот график демонстрирует еще большее несоответствие расчетных и опытных данных. К указанной ранее случайной ошибке (мере индивидуального рассеяния)
в соответствии с уравнением (2.123) составляет лишь 1.32 раза. На рис. 2.22 расчетные данные по формуле (2.123) представлены линиями 4 и 5 для алюминиевых сплавов и сталей соответственно. Этот график демонстрирует еще большее несоответствие расчетных и опытных данных. К указанной ранее случайной ошибке (мере индивидуального рассеяния) 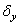 =0.43 добавляется систематическая
=0.43 добавляется систематическая 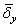 =0.5.
=0.5.
Расчетные значения коэффициента 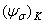 по уравнению (2.123) для алюминиевых сплавов в 1,5...2 раза меньше опытных данных. Аналогичные результаты следует ожидать и для других конструкционных материалов.
по уравнению (2.123) для алюминиевых сплавов в 1,5...2 раза меньше опытных данных. Аналогичные результаты следует ожидать и для других конструкционных материалов.
Для всех рассмотренных групп конструкционных материалов чувствительность к асимметрии цикла напряжений при наличии концентратора монотонно убывает с ростом статической прочности, как это отмечалось и для гладких образцов.
Метод расчетного построения диаграммы предельных амплитуд образцов с концентрацией напряжений автора [11], рассмотренный выше, приводит в пределах упругого деформирования (участок A1B1 на рис. 2.20) к уравнению диаграммы следующего вида
 , (2.124)
, (2.124)
которое определяет расчетную формулу для 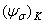 ,
,
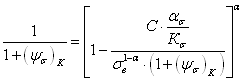 . (2.125)
. (2.125)
Как следует из уравнения (2.125), коэффициент чувствительности материала к асимметрии цикла напряжений зависит от чувствительности материала к концентрации напряжений, что учитывается в указанном уравнении наличием отношения 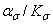 .
.
Вычисленные значения 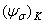 для рассматриваемых групп конструкционных материалов приведены в таблице 2.13. На рис. 2.23 для наглядности показана зависимость
для рассматриваемых групп конструкционных материалов приведены в таблице 2.13. На рис. 2.23 для наглядности показана зависимость 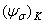 от предела прочности сталей для различных значений отношения
от предела прочности сталей для различных значений отношения 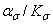 .
.
Для материалов, абсолютно чувствительных к концентрации напряжений, то есть при  , формула (2.125) полностью совпадает с уравнением (2.75), что говорит о независимости коэффициента чувствительности к асимметрии цикла напряжений от степени концентрации напряжений, то есть
, формула (2.125) полностью совпадает с уравнением (2.75), что говорит о независимости коэффициента чувствительности к асимметрии цикла напряжений от степени концентрации напряжений, то есть 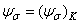 .
.
Экспериментальные данные, ранее представленные на рис. 2.22, показаны на рис. 2.24 в координатах 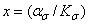 ,
,  .
.
Таблица 2.13. Значения коэффициента чувствительности к асимметрии цикла напряжений  , вычисленные по формуле (2.125).
, вычисленные по формуле (2.125).
| Материал | 
| 1,00 | 1,05 | 1,10 | 1,20 | 1,30 | 1,50 | 2,00 |
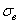 , МПа , МПа
| ||||||||
| алюминиевые сплавы | 0,420 | 0,443 | 0,465 | 0,512 | 0,558 | 0,653 | 0,898 | |
| 0,319 | 0,336 | 0,353 | 0,388 | 0,423 | 0,493 | 0,676 | ||
| 0,272 | 0,286 | 0,301 | 0,330 | 0,360 | 0,419 | 0,573 | ||
| 0,243 | 0,256 | 0,269 | 0,295 | 0,321 | 0,374 | 0,510 | ||
| 0,223 | 0,234 | 0,246 | 0,270 | 0,294 | 0,342 | 0,467 | ||
| 0,207 | 0,218 | 0,229 | 0,251 | 0,274 | 0,319 | 0,434 | ||
| 0,195 | 0,206 | 0,216 | 0,237 | 0,258 | 0,300 | 0,408 | ||
| титановые сплавы | 0,423 | 0,445 | 0,466 | 0,510 | 0,554 | 0,642 | 0,865 | |
| 0,387 | 0,407 | 0,427 | 0,467 | 0,507 | 0,587 | 0,791 | ||
| 0,365 | 0,384 | 0,403 | 0,440 | 0,478 | 0,554 | 0,746 | ||
| 0,349 | 0,367 | 0,385 | 0,421 | 0,457 | 0,530 | 0,714 | ||
| 0,338 | 0,355 | 0,372 | 0,407 | 0,442 | 0,512 | 0,689 | ||
| 0,328 | 0,345 | 0,362 | 0,395 | 0,429 | 0,497 | 0,669 | ||
| 0,320 | 0,336 | 0,353 | 0,386 | 0,419 | 0,485 | 0,653 | ||
| стали | 0,489 | 0,515 | 0,540 | 0,591 | 0,642 | 0,745 | 1,005 | |
| 0,430 | 0,453 | 0,475 | 0,519 | 0,564 | 0,654 | 0,882 | ||
| 0,399 | 0,420 | 0,440 | 0,482 | 0,523 | 0,607 | 0,818 | ||
| 0,379 | 0,398 | 0,417 | 0,457 | 0,496 | 0,575 | 0,775 | ||
| 0,363 | 0,382 | 0,401 | 0,438 | 0,476 | 0,552 | 0,743 | ||
| 0,351 | 0,369 | 0,387 | 0,424 | 0,460 | 0,533 | 0,718 | ||
| 0,341 | 0,359 | 0,376 | 0,412 | 0,447 | 0,518 | 0,698 |
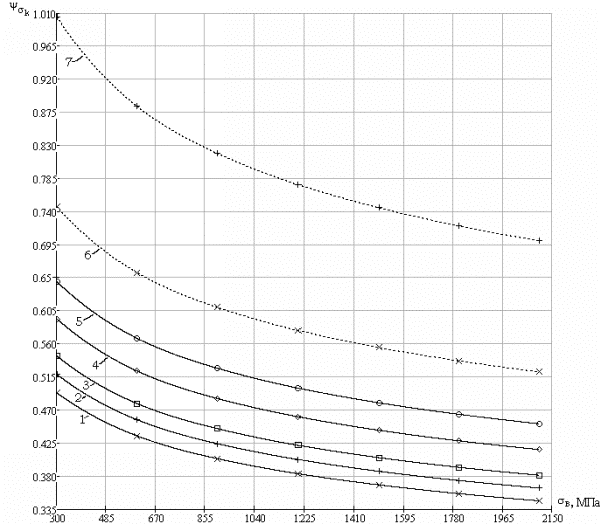
Рис. 2.23 Зависимость коэффициента чувствительности к асимметрии цикла напряжений от предела прочности сталей в связи с влиянием концентрации напряжений:
1, 2, 3, 4, 5, 6, 7 – соответственно для 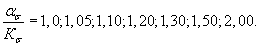
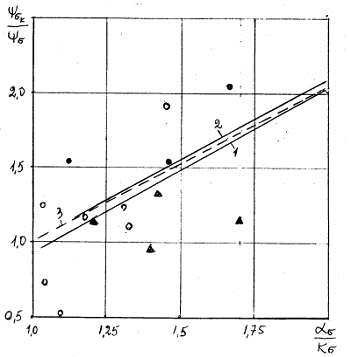
Рис. 2.24 Зависимость отношения 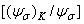 от величины
от величины 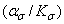 :
:
Точки — эксперимент: 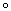 — алюминиевые сплавы,
— алюминиевые сплавы,  — титановые сплавы,
— титановые сплавы,  — стали;
— стали;
Линии — расчет: 1 — на основании регрессионного анализа (линия регрессии), 2 и 3 — по уравнениям (2.125) и (2.126) соответственно для алюминиевых сплавов и сталей.
Корреляционный и регрессионный анализы этих данных указывают на наличие достаточно тесной корреляционной связи между величинами x и у. Коэффициент корреляции достиг значения r=0.514, что больше критического значения r0.95=0.457 для уровня значимости  =0.05 [4]. Мера индивидуального рассеивания снизилась до
=0.05 [4]. Мера индивидуального рассеивания снизилась до 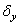 =0.367, хотя сохранилась достаточно высокой, что, как уже отмечалось выше, связано с возможными ошибками при испытании на усталость при растяжении-сжатии образцов с концентраторами напряжений.
=0.367, хотя сохранилась достаточно высокой, что, как уже отмечалось выше, связано с возможными ошибками при испытании на усталость при растяжении-сжатии образцов с концентраторами напряжений.
Таким образом, для реальных конструкционных материалов, у которых 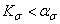 , коэффициент чувствительности к асимметрии цикла напряжений при наличии концентратора увеличивается по сравнению с соответствующим значением для гладких образцов, и это увеличение тем больше, чем ниже чувствительность материала к концентрации напряжений.
, коэффициент чувствительности к асимметрии цикла напряжений при наличии концентратора увеличивается по сравнению с соответствующим значением для гладких образцов, и это увеличение тем больше, чем ниже чувствительность материала к концентрации напряжений.
Анализ расчетных данных по формуле (2.125) (таблица 2.13) и результатов регрессионного анализа показал, что вычисление 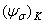 можно производить по линейному соотношению
можно производить по линейному соотношению
 , (2.126)
, (2.126)
где К — поправочный коэффициент, равный 0.05; 0.04; 0.10 для сталей, титановых и алюминиевых сплавов соответственно.
Это уравнение не дает систематической ошибки, поскольку ее графики (2 и 3 на рис. 2.24) практически совпадают с линией регрессии (1 на рис. 2.24).
Среднее квадратическое отклонение экспериментальных результатов от рассчитанных по уравнениям (2.125) и (2.126) составляет 30...40%, при этом нужно иметь в виду, что экспериментальная ошибка при оценке 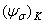 путем непосредственных испытаний на усталость заметно превышает эту величину.
путем непосредственных испытаний на усталость заметно превышает эту величину.
Приведенные данные указывают на значительное преимущество теоретического метода определения коэффициентов чувствительности к асимметрии цикла нагружения  и
и 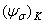 перед экспериментальным.
перед экспериментальным.
Расчетный метод оценки коэффициента чувствительности к асимметрии цикла нагружения при наличии концентрации напряжений является значительно более надежным, чем другие расчетные методы (Серенсена-Кинасошвили, Ганна, Хейвуда), что определяется более обоснованной методикой построения диаграммы предельных амплитуд при наличии концентрации напряжений, изложенной в методе Степнова М.Н.
Итак, подводя итог этого параграфа необходимо отметить, что наличие концентрации напряжений увеличивает чувствительность конструкционных материалов к асимметрии цикла нагружения, которая снижается по мере роста статической прочности материала. В связи с этим возникает необходимость корректировки соответствующего раздела ГОСТа 25.504-82.
Дата добавления: 2015-08-08; просмотров: 1162;
