Метод Р. Хейвуда

Расчетный метод Р. Хейвуда базируется на использовании уравнений (2.52) и (2.53).

На рис. 2.6 приведены для сравнения диаграммы предельных амплитуд рассчитанные методами М.Н. Степнова и Р. Хейвуда, и экспериментальные значения для сплава 7075-Т6 [13].

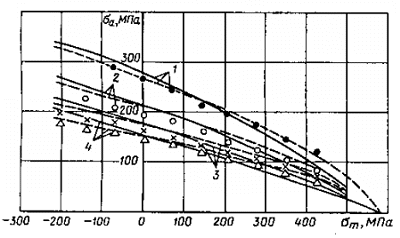
Рис.2.6. Диаграммы предельных амплитуд для сплава 7075-Т6:
штриховая линия – расчет по уравнению (2.55), сплошная – по уравнению (2.53); точки – эксперимент;
база испытаний N=10⁵ (1), 10⁶ (2), 10⁷ (3) и 10⁸ (4) циклов.

Как следует из приведенного графика оба метода удовлетворительно описывают диаграмму предельных амплитуд цикла напряжений как в области положительных значений 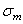, так и в области отрицательных , хотя, как было установлено, метод М.Н. Степнова с большей точностью позволяет оценивать предельную амплитуду цикла напряжений, чем метод Р. Хейвуда.

Из других известных уравнений диаграммы предельных амплитуд удовлетворительное соответствие с опытными данными имеет уравнение И.А. Биргера (1.12) и уравнение Петерсона (1.11), хотя их точность заметно ниже уравнения М.Н. Степнова (2.59). Уравнения Гудмана, Гербера и И.А. Одинга и др. из-за больших погрешностей не могут быть рекомендованы для построения диаграммы предельных амплитуд цикла напряжений.