Метод Степнова М.Н. Расчетный метод М.Н. Степнова базируется на уравнении диаграммы предельных амплитуд цикла напряжений в виде

Расчетный метод М.Н. Степнова базируется на уравнении диаграммы предельных амплитуд цикла напряжений в виде

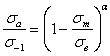, (2.58)

которое получается путем деления уравнения (2.33) на уравнение (2.3) [1], где 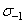- предел выносливости при симметричном цикле напряжения для выбранной базы (долговечности). Значения параметра для основных классов конструкционных материалов приведены в таблице (2.3).

Формулу для расчета предельной амплитуды цикла напряжений применительно к сталям, а также деформируемым алюминиевым и титановым сплавам для базы N = 10⁷циклов, получают путем подстановки в уравнение (2.58) расчетного значения предела выносливости при симметричном цикле нагружения по формуле (2.3)

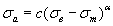(2.59)

Значения параметров (2.59) приведены в таблице 2.3.

Таблица 2.3 Значения параметров С и уравнений (2.58) и (2.59) для разных классов конструкционных материалов

Материал		С	Источник
при переменном изгибе	при переменном растяжении-сжатии
Углеродистая сталь	0,850	1,23	1,13	[5]
Легированная сталь	0,777	2,21	2,02	[5]
Общая совокупность сталей	0,820	1,75	1,60	[5]
Титановые сплавы*	0,831	1,55	1,29	[6]
Алюминиевые сплавы*	0,630	3,49	3,33	[1,5,10,11,12]
Примечание: * для базы Nб = 107 циклов.

Применительно к деформируемым алюминиевым и титановым сплавам расчет предельной амплитуды цикла напряжений для произвольной базы осуществляется соответственно по формулам (2.54), (2.55) и (2.56), (2.57).

Структура уравнения (2.58) предполагает независимость диаграммы предельных амплитуд, построенной в относительных координатах 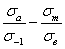, от базы испытаний.

Для проверки этого положения был проведен однофакторный дисперсионный анализ [4] экспериментальных данных, который показал, что диаграмма предельных амплитуд в указанных координатах является единой для всех рассмотренных баз испытаний (N=10⁵...10⁸ циклов). Этот вывод иллюстрирует рисунок 2.5 применительно к сплаву 7075-Т6 с 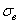= 576 МПа [13].

Как видно из графика все экспериментальные точки ложатся на общую кривую, построенную по уравнению (2.58).

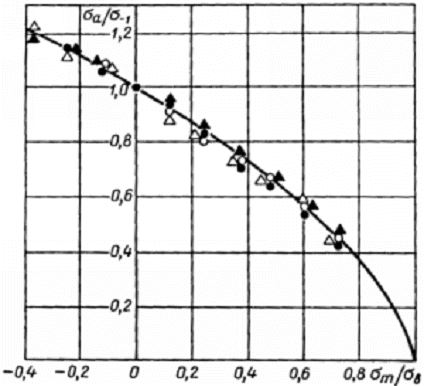
Рис.2.5. Диаграмма предельных амплитуд для сплава 7075-Т6 в относительных координатах: 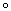, , — экспериментальные точки соответственно для баз испытания 10⁵, 10⁶, 10⁷ и 10⁸ циклов; сплошная линия – расчет по уравнению (2.58).

Правомочность высказанной ранее гипотезы о характере влияния среднего напряжения на величину предельной амплитуды цикла, т. е. адекватность уравнения (2.33) опытным данным, была дополнительно проверенна на основании 93 кривых усталости 26 вариантов деформируемых алюминиевых сплавов и их состояний. Для этой цели уравнение (2.58) путем логарифмического преобразования было приведено к линейному виду.

(2.60)

где

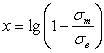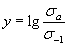, и .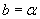

Регрессионный анализ упомянутых экспериментальных данных [4] показал адекватность уравнения (2.60) экспериментальным данным для всех рассмотренных баз испытаний (N_б = 10⁵, 10⁶, 10⁷ и 10⁸ циклов) с высоким уровнем значимости, а оценка параметра , произведенная в соответствии с методом наименьших квадратов по формуле

, (2.61)

оказалась в среднем равной 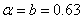для всех упомянутых баз испытаний с колебаниями не превышающими одного среднего квадратического отклонения значения параметра.

Это обстоятельство дополнительно подтверждает независимость диаграммы предельных амплитуд, построенной в относительных координатах 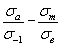, от базы испытаний (см. рис.2.5).

Уравнения (2.58) и (2.59), как показал анализ опытных данных для алюминиевых сплавов, удовлетворительно согласуется с результатами экспериментов и отрицательных средних напряжениях, если 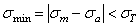, где 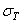- предел текучести материала.