Расчет предельной амплитуды цикла по методу М.Н. Степнова

В основу метода расчетной оценки предельной амплитуды цикла напряжений положена, выдвинутая М.Н. Степновым [1], гипотеза о том, что изменение предельной амплитуды из-за влияния среднего напряжения цикла, эквивалентно изменению предела выносливости материала при симметричном нагружении за счет снижения его предела прочности на величину, равную среднему напряжению цикла.

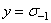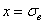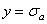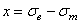Правомерность выдвинутой гипотезы вытекает из результатов экспериментов, представленных на рис. 2.4, где совмещены две зависимости в координатах и (светлые точки) и в координатах и (темные точки). Темные точки, соответствующие асимметричному нагружению, более или менее равномерно перемешиваются со светлыми точками, соответствующими результатам экспериментов при симметричном растяжении-сжатии, и описываются единым уравнением . Если принять в качестве указанной функции при симметричном нагружении уравнение (2.3), то для асимметричного нагружения получим зависимость,

, (2.33)

которая и позволяет оценивать предельные амплитуды цикла напряжений.

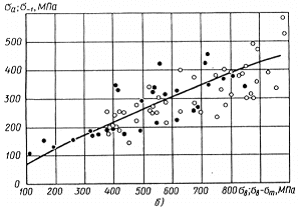
Рис.2.4 Зависимости предела выносливости от предела прочности (светлые точки) и предельной амплитуды от разности предела прочности и среднего напряжения цикла (темные точки) для алюминиевых сплавов (база N=10⁷ циклов) (а) и сталей (б); сплошная линии – расчет по уравнению (2.33); точки – экспериментальные значения.

Для конкретных конструкционных материалов и видов напряжения уравнения типа (2.33) приведены в таблице 2.2

Таблица 2.2 Уравнения для расчета предельных амплитуд цикла напряжений для конструкционных материалов

№ п/п	Материал	Вид деформаций
Асимметричный изгиб	Асимметричное растяжение- сжатие
	Деформируемые алюминиевые сплавы*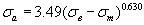
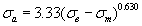
	Деформируемые титановые сплавы*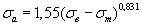
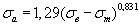
	Углеродистые стали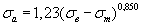
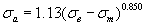
	Легированные стали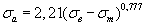
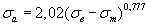
	Объединенная совокупность сталей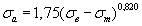
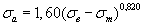
Примечание: * для базы Nб = 107 циклов

Как показал статистический анализ расчетных и экспериментальных значений предельных амплитуд цикла напряжений, использование уравнений, приведенных в таблице 2.2, повышает относительную ошибку оценивания по сравнению с формулами (2.6) - (2.10) и (2.19) - (2.23) ещё лишь на 2.3%, что дополнительно подчеркивает правомочность использованной гипотезы.