Метод М.Н. Степнова - С.П. Евстратовой

Метод М.Н. Степнова – С.П.Евстратовой построения кривой усталости для деформируемых алюминиевых сплавов базируется на понятии обобщенной кривой усталости

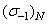Если для указанных сплавов ординаты точек кривой усталости представить в виде отношения , где и 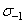— пределы ограниченной выносливости соответственно для заданной долговечности N и долговечности базы N=10⁷ циклов, то для всех деформируемых алюминиевых сплавов кривые усталости практически совпадают друг с другом и описываются единым уравнением, называемым уравнением обобщенной кривой усталости [1],

(2.38)

С учетом (2.6) и (2.22) уравнение (2.38) принимает вид

(2.39)

для переменного изгиба и

(2.40)

для переменного растяжения-сжатия.

Сходимость расчетных значений с использованием формул (2.39) и (2.40) с экспериментальными вполне удовлетворительная (относительная средняя квадратическая ошибка составляет 10% при отсутствии систематической ошибки).

Как показали дальнейшие исследования [2], метод М.Н.Степнова - С.П.Евстратовой применим и для деформируемых титановых сплавов.

Для обоснования уравнения обобщенной кривой усталости титановых сплавов [2] из ряда литературных источников, включающих и исследования автора, были отобраны построенные экспериментальным путем кривые усталости при переменном изгибе, протяженностью от 10⁵ до 10⁸ циклов нагружений (анализировалось 92 значения предела ограниченной выносливости для различных баз). Предел прочности рассматриваемых сплавов находился в диапазоне от 700 до 1300 МПа.

Предварительный графический анализ показал, что применительно к титановым сплавам также, как и для алюминиевых, имеет место обобщенная кривая усталости, построенная в координатах [1].

Использование статистического анализа вышеупомянутых экспериментальных результатов показало, что из всех известных уравнений кривых усталости наиболее адекватны опытным данным с достаточно высоким уровнем значимости являются следующие уравнения:

ранее обоснованное для алюминиевых сплавов [1] в виде

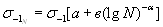(2.41)

и уравнение Штромейера (1.3)

, (2.42)

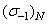где и 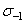— соответственно пределы ограниченной выносливости для произвольной базы N и базы N_б=10⁷ циклов, a, b, c, d, , 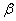— параметры уравнений.

С помощью регрессионного анализа [4] была произведена оценка указанных параметров. Окончательно уравнения кривых усталости при переменном изгибе для титановых сплавов представляются в виде

(2.43)

и

(2.44)

Как показывают расчеты, расхождение в ординатах кривых усталости, построенных по этим уравнениям, в диапазоне долговечности 10⁵...10⁹ циклов не превышает 1%, а при расхождение между ними чуть выше 2%. Таким образом, в статистическом плане эти уравнения равноценны. На практике же следует отдать предпочтение первому уравнению, обеспечивающему более надежные результаты при прогнозировании сопротивления усталости на больших долговечностях.

Относительное среднее квадратическое отклонение расчетных значений 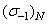по уравнениям (2.43) и (2.44) от экспериментальных данных при долговечности 10⁵ циклов составляет около 6%, и для долговечностей в диапазоне 10⁶...10⁸ циклов – не превышает 3%.

Уравнения (2.43) и (2.44) содержат единственный неизвестный параметр, поэтому они позволяют построить кривые усталости по результатам испытаний лишь на одном уровне амплитуды цикла напряжений, что обеспечит значительное сокращение временных и материальных затрат на проведения испытаний.

Установленные ранее [6] корреляционное соотношение (2.7) между пределом ограниченной выносливости при переменном изгибе для базы 10⁷ циклов и пределом статической прочности титановых сплавов

,

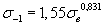открывает возможность построения кривых усталости расчетным методом на основании данных о статической прочности сплавов.

Применительно к симметричному циклу переменного изгиба уравнения кривых усталости (2.43) и (2.44) с учетом (2.7) примут вид

(2.45)

(2.46)

Относительное среднее квадратическое отклонение ординат экспериментальной кривой усталости от расчетных значений по уравнениям (2.45) и (2.46) составляет около 15%. Следует иметь в виду, что средняя квадратическая погрешность экспериментального определения медианы предела выносливости или предельной амплитуды цикла напряжений при испытании на усталость 8...10 образцов на одну кривую, как того требует существующий стандарт, соизмерима с величиной коэффициента вариации предела выносливости, который для титановых сплавов составляет 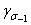=7..15%.

Таким образом, предложенный метод расчетного построения кривых усталости для титановых сплавов по своей точности соизмерим с экспериментальным методом.

Проведенный анализ результатов отечественных и зарубежных исследований показал, что отношение пределов ограниченной выносливости при симметричном растяжении-сжатии и переменном изгибе 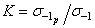образцов из титановых сплавов слабо зависит от базы испытаний и составляет в среднем 0.829 [6]. В связи с этим и в соответствии с формулой (2.7) оценка предела выносливости при симметричном растяжении-сжатии лабораторных образцов при отсутствии концентрации напряжений для титановых сплавов на базе 10⁷ циклов может быть произведена по формуле (2.23).

Уравнения обобщенной кривой усталости (2.43) и (2.44) и соотношение (2.33) позволяют строить кривую усталости для симметричного растяжения-сжатия образцов из титановых сплавов расчетным способом по уравнениям

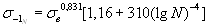(2.47)

и

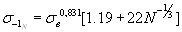. (2.48)

Относительное среднее квадратическое отклонение расчетных значений предельных амплитуд напряжений по уравнениям (2.47) и (2.48) и экспериментальных результатов с учетом наблюдаемой дисперсии отношения 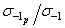составляет 17%, что лишь на 2...5% превышает относительную среднюю квадратическую ошибку экспериментального определения предела выносливости при переменном растяжении-сжатии путем испытания на усталость серии из 8...10 образцов.