Расчет предела выносливости материала при симметричном цикле напряжений

Длительность и высокая стоимость испытаний на усталость побудили появление косвенных методов оценки предела выносливости материала, базирующихся на результатах статических испытаний материала и применении корреляционного и регрессионного анализа опытных данных.

Как показали результаты многочисленных исследований отечественных и зарубежных ученых, предел выносливости имеет тесную корреляционную связь с пределом прочности (временным сопротивлением) при статическом нагружении. На начальной стадии изучения сопротивления усталости материала предел выносливости сталей выражали как некую долю предела прочности,

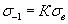(2.1)

В капитальной монографии английского ученого Р.Хейвуда [3], например, принято, что отношение предела выносливости при симметричном растяжении-сжатии к пределу прочности сталей, равно K=0,5. С учетом этого отношения им были разработаны методы оценки прочности деталей и элементов конструкций, обеспечивающие для того времени достаточную надежность инженерных решений.

Среди отечественных ученых наиболее серьезные исследования связей между усталостными и статическими характеристиками сталей выполнил С.Л.Жуков, который в послевоенные годы (1945 - 1947 гг.) опубликовал серию статей, посвященную этой проблеме.

В качестве основного уравнения линии регрессии С.Л.Жуковым и целым рядом других последователей использовалось линейное уравнение вида

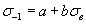(2.2)

В ряде работ использовались линейные уравнения двумерной и многомерной регрессии, связывающие предел выносливости сталей с характеристиками прочности и пластичности.

Ниже для примера приведены наиболее характерные уравнения, предложенные рядом авторов, для оценки предела выносливости при симметричном изгибе с вращением,

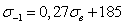(С.Л.Жуков)

(С.Л.Жуков)

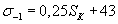(С.Л.Жуков)

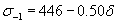(С.Л.Жуков)

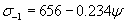(С.Л.Жуков)

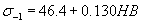(В.М.Гребеник)

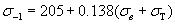(С.Л.Жуков)

(М.П.Марковец)

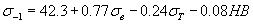(В.М.Гребеник)

Все эти уравнения, а также уравнения (2.1) и (2.2), имеют два серьезных недостатка. Во-первых, в работах указанных и других авторов рассматривается лишь линейный характер связи между механическими характеристиками и без какого-либо обоснования игнорируется нелинейная зависимость, которая, как показывает регрессионный анализ [4], более адекватна опытным данным. Во-вторых, из-за относительно ограниченного объема статистического материала в этих работах недостаточно внимания уделено надежному обоснованию средней квадратической ошибки оценивания предела выносливости и её зависимости от уровня прочности материала, что не позволяет оценивать нижние (гарантированные) значения 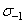материалов различной прочности.