Расчет винтовых пружин с малым шагом витков

Винтовая пружина представляет собой тонкий стержень, чаще всего круглого сечения, ось которого является винтовой линией. Винтовые пружины применяются в вагонных рессорах и различных деталях машин и механизмов. Для пружин с малым шагом витков (рис.5.38, а) соблюдается условие

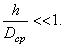(5.38)

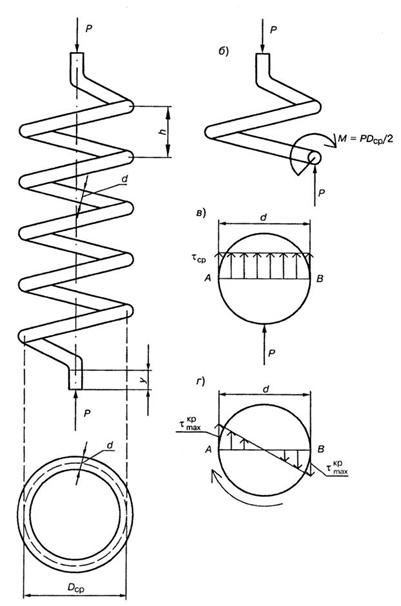
Рис. 5.38

Здесь 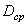- средний диаметр пружины, т.е. диаметр цилиндра, на котором лежит винтовая ось пружины. Таким образом, в этом случае, можно приближенно считать, что плоскость витка горизонтальна. Несмотря на сравнительную сложность формы оси, нетрудно вывести формулы для приближенного расчета пружин с малым шагом. При действии сил, направленных по оси пружины и растягивающих или сжимающих ее, стержень пружины в основном испытывает кручение.

Проведем в каком-либо месте разрез стержня пружины вертикальной плоскостью, проходящей через ось пружины (рис.5.38, б) и отбросим нижнюю часть. При условии (5.38) сечение приближенно можно считать не эллипсом, а кругом.

Действие отброшенной части на верхнюю сводится к силе Р, направленной вверх по оси пружины. При параллельном переносе силы Р в центр сечения стержня (рис.5.38, б) присоединится крутящая пара 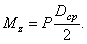Таким образом, в сечении пружины возникают два внутренних силовых фактора: поперечная сила Q=Р и крутящий момент 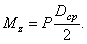Оба эти фактора вызывают в сечении касательные напряжения. Наибольшие напряжения от кручения (у контура сечения) будут равны (рис.5.38, г)

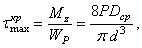(5.39)

где d – диаметр стержня пружины.

Напряжения от поперечной силы имеют наибольшую величину 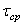вдоль горизонтального диаметра АВ сечения, где они направлены вертикально. По формуле Журавского (рис.5.38, в)

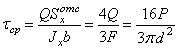. (5.40)

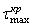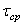Внутренняя точка А диаметра является опасной точкой сечения, так как здесь напряжения и совпадают по направлению и складываются. Расчетное напряжение будет

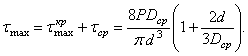(5.41)

При малом отношении можно вторым членом в скобках пренебречь по сравнению с единицей, т.е. рассчитывать пружину на одно кручение.

Если же отношение не мало (например, в вагонных рессорах и других тяжелых пружинах), то влияние поперечной силы на напряжения значительно и должно учитываться. Кроме того, в этом случае существенно сказывается влияние кривизны стержня пружины, вследствие которой напряжение от кручения у внутренней точки А сечения оказывается больше, чем у наружной точки В. Ввиду этого в правую часть формулы (5.41) вместо выражения, стоящего в скобках, лучше ввести коэффициент К, учитывающий одновременно влияние поперечной силы и кривизны стержня:

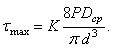(5.42)

Этот коэффициент можно вычислять по формуле

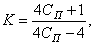(5.43)

где 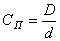- геометрический параметр пружины.

На практике нужно уметь вычислять удлинение или осадку пружины от растягивающих или сжимающих ее сил. Влияние поперечной силы на удлинение невелико, поэтому обычно принимается в расчет влияние кручения витков.

На рис.5.39 показан бесконечно малый элемент проволоки пружины 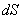, находящейся в условиях кручения. Правое сечение поворачивается на угол

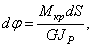
а все точки на оси перемещаются на величину

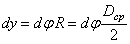. (5.44)

Суммируя эти перемещения за счет закручивания длины проволоки, получим полное сокращение расстояния между торцами пружины

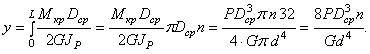(5.45)

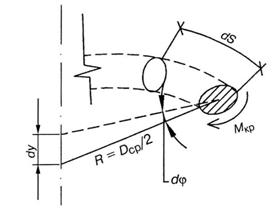
Рис. 5.39

Условие прочности пружины

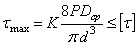(5.46)

Так как пружины должны давать достаточно большие упругие удлинения, то они изготовляются из закаленной стали с очень высоким пределом пропорциональности. Допускаемое касательное напряжение 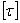колеблется при статической нагрузке от 350 МПа до 500 МПа, а для особо прочных специальных сталей – и выше. При переменной нагрузке допускаемое напряжение значительно снижается (на 30-65%).