Пример 22.

Стержень переменного сечения с соотношением площадей поперечных сечений A₁/A₂ =2 находится под действием сосредоточенных сил и собственного веса (рис. а). Материал стержня на всех участках одинаков. Требуется построить эпюры распределения продольной силы и напряжений вдоль оси стержня и определить перемещение сечения а–а.

Решение.

Строим эпюры изменения продольной силы и напряжений вдоль оси стержня. Собственный вес стержня принято учитывать, заменяя его распределенной по всей длине нагрузкой. Интенсивность распределенной нагрузки равна собственному весу, действующему на единицу длины стержня, т. е.

на первом и втором участках

,

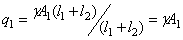на третьем участке

,

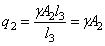где – объемный вес материала стержня.

Эпюры продольной силы и напряжений строим, используя метод сечений. Заметим, что угол наклона эпюры продольной силы зависит от величины q и, следовательно, при построении эпюры N в масштабе угол ее наклона на первом и втором участке должен быть больше, чем на третьем участке, так как A₁ по условию больше, чем A₂ (рис. б). Угол же наклона эпюры напряжений зависит от объемного веса g, и поэтому угол наклона эпюры напряжений на всех участках одинаков (рис. в).

Находим перемещение (опускание) сечения а–а. Это перемещение можно искать разными способами. По первому способу для определения перемещения используем формулу 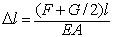. Здесь F – сосредоточенная сила, вызывающая перемещение участка длиной l; G – собственный вес рассматриваемого участка. Эту формулу можно использовать на участках постоянного сечения между сосредоточенными силами. Отсчет надо вести от неподвижного сечения, т.е. заделки. Например, в рассматриваемой задаче перемещение сечения а–а складывается из удлинения участка длиной l₁, которое мы обозначим 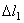, и удлинения участка длиной 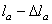. При определении удлинения 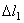в формуле сила F равна сумме F₁, F₂ и собственного веса всех расположенных ниже участков. Вес участка стержня длиной l₁: 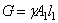. Таким образом, по формуле

.

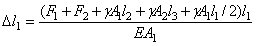Удлинение 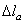происходит под действием сосредоточенной силы, состоящей из силы F₂, веса участков стержня, расположенных ниже сечения а–а, и собственного веса участка 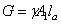. То есть

.

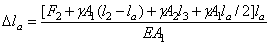Окончательно опускание сечения а–а равно .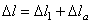

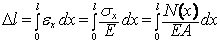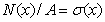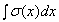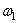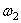Если построена эпюра распределения напряжений, то для определения перемещения заданного сечения удобно использовать второй способ, применяя формулу . В этой формуле , а – это площадь эпюры напряжений. Таким образом, если найти площадь двух трапеций на участке между неподвижным сечением (заделкой) и сечением а–а (заштрихованные площади и эпюры 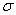на рис. в)и разделить полученную величину на модуль упругости, мы получим искомое перемещение сечения а–а:

.

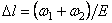При вычислении перемещения обращайте внимание на единицы измерения величин, входящих в формулы. Рекомендуем окончательный результат получить в сантиметрах.