Пример 8. Построить эпюру Nz для стержня, приведенного на рисунке.

Построить эпюру N_z для стержня, приведенного на рисунке.

Р е ш е н и е.

Стержень нагружен только сосредоточенными осевыми силами, поэтому продольная сила в пределах каждого участка постоянна. На границе участков N_zпретерпевает разрывы. Примем направление обхода от свободного конца (сеч. Е) к защемлению (сеч. А). На участке DE продольная сила положительна, так как сила вызывает растяжение, т.е. N_ED = +F. В сечении D продольная сила меняется скачком от N_DE = N_ED = F до N_DС = N_DЕ –3F = –2F (находим из условия равновесия бесконечно малого элемента dz, выделенного на границе двух смежных участков CD и DE).

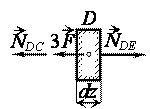
Заметим, что скачок равен по величине приложенной силе 3F и направлен в сторону отрицательных значений N_z, так как сила 3F вызывает сжатие. На участке CDимеем N_СD = N_DС = –2F. В сечении C продольная сила изменяется скачком от N_СD = –2F до N_СВ = N_СD + 5F = 3F. Величина скачка равна приложенной силе 5F. В пределах участка CВ продольная сила опять постоянна N_СВ = N_ВС =3F. Наконец, в сечении В на эпюре N_z опять скачок: продольная сила меняется от N_ВС = 3F до N_ВА = N_ВС –2F = F. Направление скачка вниз (в сторону отрицательных значений), так как сила 2F вызывает сжатие стержня. Эпюра N_z приведена на рисунке.