Деформации и перемещения. Закон Гука
Рассмотрим однородный стержень с одним концом, жестко заделанным, и другим - свободным, к которому приложена центральная продольная сила Р (рис. 2.8). До нагружения стержня его длина равнялась 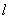 - после нагружения она стала равной
- после нагружения она стала равной  (рис. 2.8). Величину
(рис. 2.8). Величину 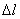 называют абсолютным удлинением стержня.
называют абсолютным удлинением стержня.
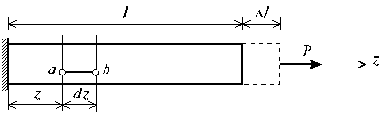
Рис. 2.8
Если в нагруженном стержне напряженное состояние является однородным, т.е. все участки стержня находятся в одинаковых условиях, деформация 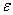 остается одной и той же по длине стержня и равной
остается одной и той же по длине стержня и равной
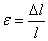 . (2.4)
. (2.4)
Если же по длине стержня возникает неоднородное напряженное состояние, то для определения его абсолютного удлинения необходимо рассмотреть бесконечно малый элемент длиной dz (рис. 2.8). При растяжении он увеличит свою длину на величину 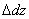 и его деформация составит:
и его деформация составит:
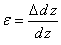 . (2.5)
. (2.5)
В пределах малых деформаций при простом растяжении или сжатии закон Гука записывается в следующем виде (нормальные напряжения в поперечном сечении прямо пропорциональны относительной линейной деформации 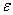 ):
):
 . (2.6)
. (2.6)
Величина Е представляет собой коэффициент пропорциональности, называемый модулем упругости материала первого рода (модуль продольной упругости). Его величина постоянна для каждого материала. Он характеризует жесткость материала, т.е. способность сопротивляться деформированию под действием внешней нагрузки.
Из совместного рассмотрения уравнений (2.5) и (2.6) получим:
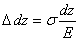 ,
,
откуда с учетом того, что
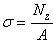 и
и 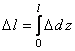 ,
,
окончательно получим:
 . (2.7)
. (2.7)
Если стержень изготовлен из однородного изотропного материала с Е = const, имеет постоянное поперечное сечение A = const и нагружен по концам силой Р, то из (2.7) получим
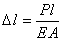 . (2.8)
. (2.8)
Зависимость (2.8) также выражает закон Гука. Знаменатель EA называется жесткостью при растяжении - сжатии или продольной жесткостью.
При решении многих практических задач возникает необходимость, наряду с удлинениями, обусловленными действием механических нагрузок, учитывать также удлинения, вызванные температурным воздействием. В этом случае пользуются принципом независимости действия сил, и полные деформации рассматривают как сумму силовой и температурной деформаций:
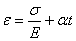 , (2.9)
, (2.9)
где  - коэффициент температурного расширения материала; t -перепад температуры тела. Для однородного стержня, нагруженного по концам продольными силами Р и равномерно нагретого по длине, получим:
- коэффициент температурного расширения материала; t -перепад температуры тела. Для однородного стержня, нагруженного по концам продольными силами Р и равномерно нагретого по длине, получим:
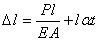 . (2.10)
. (2.10)
Дата добавления: 2015-08-08; просмотров: 2140;
