Пример 1. Пусть имеется стержень постоянного поперечного сечения, нагруженный силами 2Р и 3Р вдоль продольной оси стержня

Пусть имеется стержень постоянного поперечного сечения, нагруженный силами 2Р и 3Р вдоль продольной оси стержня, показанный на рис.2.3. Определить величину внутренних сил.

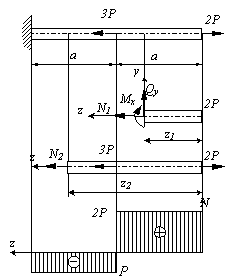
Рис.2.3

Решение.

Стержень может быть разделен на два участка, граничными точками которых являются точки приложения сосредоточенных сил и точка закрепления. Если начало координат расположить на правом конце стержня, а ось z направить справа налево, то, используя метод сечений, рассекая последовательно участки, отбрасывая левую часть,заменяя ее действие внутренними усилиями N, Q_y, M_x и уравновешивая оставшуюся часть, получим:

I участок: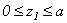

, ;

, ;

,

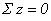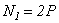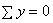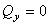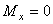
Как видно, при растяжении в поперечных сечениях стержня возникает только один внутренний силовой фактор - нормальная сила N.

II участок: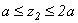

, .

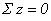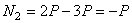Таким образом, нормальная сила равна алгебраической сумме проекций сил, приложенных к отсеченной части на продольную ось .

Полученные результаты для большей наглядности удобно представить в виде графика, (эпюры N), показывающего изменение продольной силы вдоль оси стержня (рис.2.3). Построим на первом участке линию параллельную оси z на высоте 2Р, на втором участке – линию со значением -Р. Области ограниченные графиком и осью zпринято штриховать и обозначать знак этой области. Видно, что наибольшая продольная сила возникает на первом участке стержня и, как следствие, при прочих равных условиях, он скорее может разрушиться, чем второй участок.