Продольные силы в поперечных сечениях

Под растяжением (сжатием) понимают такой вид нагружения, при котором в поперечных сечениях стержня возникают только продольные силы , а прочие силовые факторы равны нулю.

Рассмотрим однородный прямолинейный стержень длиной 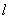и площадью поперечного сечения А, на двух концах которого прило­жены две равные по величине и противоположно направленные центральные продольные силы Р (рис. 2.2, а).

Продольная сила – внутреннее усилие, равное сумме проекций всех внешних сил, взятых с одной стороны от сечения, на ось стержня. Примем следующее правило знаков для продольной силы: растягивающая продольная сила положительна, сжимающая – отрицательна (рис. 2.1).

Рис.2.1

Поместим начало плоской системы координат yz в центре тяжести левого сечения, а ось 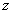направим вдоль продольной оси стержня.

Для определения величин внутренних усилий воспользуемся методом сечений. Задавая некоторое сечение на расстояние z ( 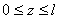) от начала системы координат и рассматривая равновесие левой относительно заданного сечения части стержня (рис. 2.2, б), приходим к следующему уравнению:

,

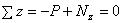откуда следует, что

.

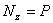Следовательно, продольная сила в сечении численно равна сумме проекций на ось стержня всех сил, расположенных по одну сторону сечения

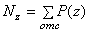(2.1)

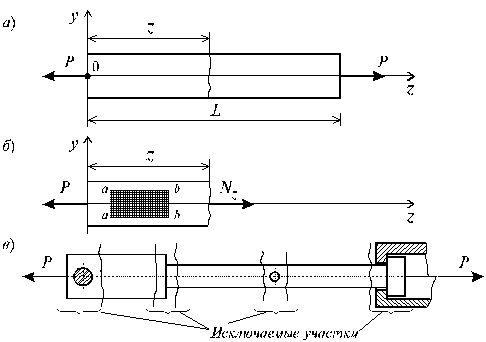
Рис. 2.2

Для наглядного представления о характере распределения продольных сил по длине стержня строится эпюра продольных сил . Осью абсцисс служит ось стержня. Каждая ордината графика – продольная сила (в масштабе сил) в данном сечении стержня.

Эпюра позволяет определить, в каком сечении действует максимальное внутреннее усилие (например, найти N_max при растяжении-сжатии). Сечение, где действует максимальное усилие будем называть опасным.

Рассмотрим несколько примеров определения внутренних сил.