Закон Гука и принцип независимости действия сил

Многочисленные экспериментальные наблюдения за поведени­ем деформируемых тел показывают, что в определенных диапазо­нах перемещения точек тела пропорциональны действующим на него нагрузкам. Впервые указанная закономерность была высказана в 1776 году английским ученым Р.Гуком и носит название закона Гука.

В соответствии с этим законом перемещение произвольно взя­той точки А (рис. 1.8, а) нагруженного тела по некоторому направ­лению, например, по оси x, а может быть выражено следующим образом:

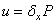, (1.11)

где Р - сила, под действием которой происходит перемещение u; - коэффициент пропорциональности между силой и перемеще­нием.

Очевидно, что коэффициент зависит от физико-механиче­ских свойств материала, взаимного расположения точки А и точки приложения и направления силы Р, а также от геометрических особенностей си­стемы. Таким образом, последнее выражение следует рассматривать как закон Гука для данной системы.

В современной трактовке закон Гука определяет линейную за­висимость между напряжениями и деформациями, а не между си­лой и перемещением.

, (1.12)

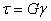. (1.13)

Параметры 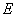и , входящие в эти формулы, называют модулями упругости материала соответственно первого и второго рода. Они характеризуют его сопротивляемость деформированию, или жесткость в упругой стадии деформации. Численные значения 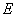и для каждого конструктивного материала определяются экспериментально. Они имеют размерности напряжений. На практике удобно использовать единицы, кратные паскалю: мегапаскаль (1 МПа=10⁶ Па) и гигапаскаль (1 ГПа=10⁹Па).

Системы, для которых соблюдается условие пропорционально­сти между напряжениями и деформациями, подчиняются принципу суперпозиции, илипринципу независимости действия сил.

В соответствии с этим принципом перемещения и внутренние силы, возникающие в упругом теле, считаются независящими от порядка приложения внешних сил. То есть, если к системе прило­жено несколько сил, то можно определить внутренние силы, на­пряжения, перемещения и деформации от каждой силы в отдель­ности, а затем результат действия всех сил получить как сумму действий каждой силы в отдельности. Принцип независимости действия сил является одним из основных способов при решении большинства задач механики линейных систем.