Изгиб балки при действии продольных и поперечных сил.

На практике очень часто встречаются случаи совместной работы стержня на изгиб и на растяжение или сжатие. Подобного рода деформация может вызываться или совместным действием на балку продольных и поперечных сил, или только одними продольными силами.

Первый случай изображен на Рис.1. На балку АВ действуют равномерно распределенная нагрузка q и продольные сжимающие силы Р.

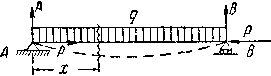
Рис.1. Совместное действие изгиба и сжатия.

Предположим, что прогибами балки по сравнению с размерами поперечного сечения можно пренебречь; тогда с достаточной для практики степенью точности можно считать, что и после деформации силы Р будут вызывать лишь осевое сжатие балки.

Применяя способ сложения действия сил, мы можем найти нормальное напряжение в любой точке каждого поперечного сечения балки как алгебраическую сумму напряжений, вызванных силами Р и нагрузкой q.

Сжимающие напряжения 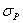от сил Р равномерно распределены по площади F поперечного сечения и одинаковы для всех сечений:

нормальные напряжения от изгиба в вертикальной плоскости в сечении с абсциссой х, которая отсчитана, скажем, от левого конца балки, выражаются формулой

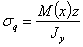
Таким образом, полное напряжение в точке с координатой z (считая от нейтральной оси) для этого сечения равно

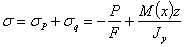
На Рис.2 изображены эпюры распределения напряжений в рассматриваемом сечении от сил Р, нагрузки q и суммарная эпюра.

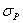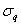Наибольшее напряжение в этом сечении будет в верхних волокнах, где оба вида деформации вызывают сжатие; в нижних волокнах может быть или сжатие или растяжение в зависимости от числовых величин напряжений и . Для составления условия прочности найдем наибольшее нормальное напряжение.

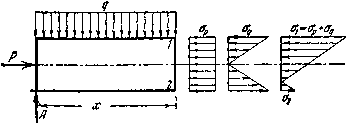
Рис.2. Сложение напряжений сжатия и изгиба

Так как напряжения от сил Р во всех сечениях одинаковы и равномерно распределены, то опасными будут волокна, наиболее напряженные от изгиба. Такими являются крайние волокна в сечении с наибольшим изгибающим моментом; для них

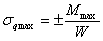
Таким образом, напряжения в крайних волокнах 1 и 2 среднего сечения балки выражаются формулой

,

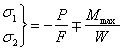и расчетное напряжение будет равно

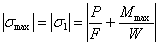
Если бы силы Р были растягивающими, то знак первого слагаемого изменился бы, опасными были бы нижние волокна балки.

Обозначая буквой N сжимающую или растягивающую силу, можем написать общую формулу для проверки прочности:

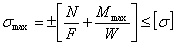
(27.1)

Описанный ход расчета применяется и при действии на балку наклонных сил. Такую силу можно разложить на нормальную к оси, изгибающую балку, и продольную, сжимающую или растягивающую.