Уравнение Бернулли. Рассмотрим течение идеальной несжимаемой жидкости по трубке тока

Рассмотрим течение идеальной несжимаемой жидкости по трубке тока. Под действием сил давления 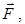действующих внутри жидкостей, большой объем V, находящийся между сечениями 1 и 2 будет перемещаться и через малый промежуток времени займет положение между сечениями 1^' и 2^' (рис. 4.1б). В условиях стационарного течения жидкости изменение энергии выделенного большого объема V будет связано только с изменением энергий, происходящих в малых объемах V₁ и V₂.

Изменение кинетической энергии этих объемов V₁ и V₂ определяется работой сил тяжести и сил давления, действующих на выделенные объемы со стороны соседних слоев жидкости. Причем работу совершают только силы давления 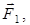и .

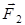Учитывая незначительность объемов V₁ и V₂, можно записать:

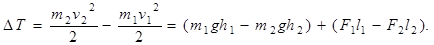
Введем в это уравнение плотность жидкости (ρ = m₁/V₁ = m₂/V₂ , m₁ = m₂, V₁ = V₂) и давление, оказываемое жидкостью на сечения 1 и 2^' объемов V₁ и V₂ (p₁ =F₁/S₁, p₂ = F₂/S₂). После несложных преобразований получим:

С учетом произвольности выбираемого объема и сечения в трубке тока окончательно можно записать следующее уравнение:

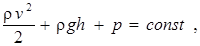(4.2)

которое получило название уравнения Бернулли.

Отдельные слагаемые в уравнении Бернулли имеют размерность давления. Принято называть давление ρv²/2– динамическим, ρgh– гидростатическим, давление р– статическим.

Уравнение Бернулли справедливо для любых точек внутри жидкости, расположенных вдоль определенной линии тока. При переходе от одной линии тока к дугой изменяются значения постоянной.