Потенциальная энергия. Потенциальной энергией можно характеризовать систему тел только в том случае, если между телами этой системы взаимодействие осуществляется посредством

Потенциальной энергией можно характеризовать систему тел только в том случае, если между телами этой системы взаимодействие осуществляется посредством консервативных сил. Силы называют консервативными, если работа этих сил не зависит от формы траектории, по которой перемещается тело, и определяется только начальным и конечным положением тала. Для консервативных сил работ на любом замкнутом пути равна нулю. Консервативными силами являются: силы тяготения, силы упругости, электростатические силы взаимодействия.

Силы, не удовлетворяющие отмеченному выше свойству, называют диссипативными силами. Сила трения – это диссипативная сила.

Назовем определенное расположение тел в пространстве конфигурацией этой системы. Каждой конфигурации соответствует свое значение потенциальной энергии U. Потенциальная энергия определяется с точностью до некоторой произвольной постоянной.

Изменение конфигурации (взаимного расположения тел) приводит к изменению потенциальной энергии системы. Увеличение потенциальной энергии системы можно осуществить только посредством положительной работы внешних сил. Работа же внутренних (консервативных) сил приводит к убыли потенциальной энергии. Работа консервативных сил при бесконечно малом изменении конфигурации является полным дифференциалом функции U:

dA = – dU. (2.13)

Работа консервативных сил при изменения конфигурации системы тел:

А = – ∆U = U₁ – U₂.

Зная вид функции U(x,y,z), можно найти силу, действующую на частицу в каждой точке поля. Рассмотрим перемещение частицы в произвольном направлении. Такое перемещение сопровождается совершением над частицей работы 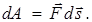В направлении оси хсила 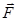совершит работу 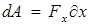. Согласно (2.13) та же работа может быть представлена как убыль потенциальной энергии: 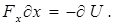Откуда

Для компонент силы по осям yи zполучаются аналогичные выражения. Таким образом,

, ,

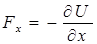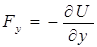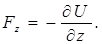
Зная компоненты, можно найти вектор силы:

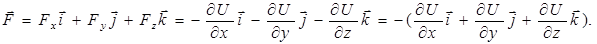
Выражение, стоящее в скобках, обозначим символом

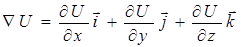(2.14)

и назовем градиентом потенциальной энергии.

Таким образом

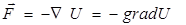(2.15)

Градиент потенциальной энергии это вектор, модуль который равен консервативной силе, действующей на тело. Этот вектор указывает направление в котором потенциальная энергия увеличивается с наибольшей скоростью.

Можно показать, что в замкнутой консервативной системе полная механическая энергия, состоящая из кинетической и потенциальной энергии, сохраняется:

Е = Т + U = const, (2.16)

т.е. в замкнутой консервативной системе механическая энергия не исчезает и не появляется вновь, она может лишь превращаться из одного вида в другой (закон сохранения механической энергии).

Лекция 3