Основное уравнение динамики вращательного движения. Если тело, закрепленное на неподвижной оси О, приходит во вращательное движение под действием некоторой силы (рис
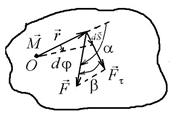
Если тело, закрепленное на неподвижной оси О, приходит во вращательное движение под действием некоторой силы 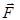 (рис. 3.3), то эта сила совершает над телом работу. Работа силы приводит к приращению кинетической энергии (dA= dT).
(рис. 3.3), то эта сила совершает над телом работу. Работа силы приводит к приращению кинетической энергии (dA= dT). 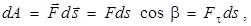
|
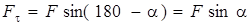 , а
, а 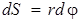
то 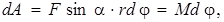 где
где 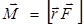 - момент силы.
- момент силы.
Модуль момента силы 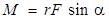 . Направление вектора
. Направление вектора 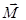 определяется по правилу правого винта (см. приложение 1). На рис. 3.3 момент силы направлен по оси вращения от нас.
определяется по правилу правого винта (см. приложение 1). На рис. 3.3 момент силы направлен по оси вращения от нас.
Так как  то
то 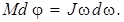 Взяв производную по времени от последнего выражения, получим:
Взяв производную по времени от последнего выражения, получим:
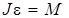 или
или 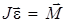 . (3.9)
. (3.9)
Записанное соотношение и называют основным уравнением динамики вращательного движения. В динамике вращательного движения используется понятие момент импульса 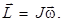
Используя это понятие основное уравнение динамики вращательного движения можно записать в виде:
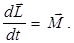 (3.10)
(3.10)
Из последнего выражения следует, что при 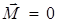 ,
,  - закон сохранения момента импульса.
- закон сохранения момента импульса.
Основные уравнения динамики поступательного и вращательного движений можно записать, используя следующие формулы:
поступательное движение вращательное движение
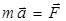 ,
, 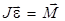 ,
,
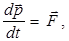
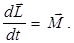
Дата добавления: 2015-08-08; просмотров: 792;
