Лекция 6/7
Основные выводы.
1. Электромагнитное поле описывается четырьмя уравнениями Максвелла:
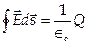 (1)
(1)
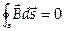 (2)
(2)
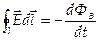 (3)
(3)
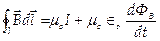 (4)
(4)
2. Уравнения Максвелла имеют следующий смысл:
Уравнение (1) — обобщенный закон Кулона, связывающий электрическое поле с его источниками — электрическими зарядами.
Уравнение (2) — математическое выражение того факта, что не существует изолированных магнитных зарядов: силовые магнитные линии замкнуты.
Уравнение (3) показывает, что изменение магнитного поля порождает электрическое поле.
Уравнение (4) показывает, что магнитное поле порождается электрическим током и изменяющимся электрическим полем.
3. Уравнения Максвелла предсказывают существование электромагнитных волн, а коэффициент 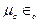 имеет размерность обратного квадрата скорости. При этом численное значение величины
имеет размерность обратного квадрата скорости. При этом численное значение величины
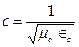
равно скорости света.
4. Цепи переменного тока, содержащие источник ЭДС, подчиняются закону 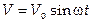 :
:
а) Цепь, содержащая активное сопротивление R:
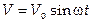 ,
, 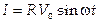 .
.
б) Цепь содержащая емкость C:
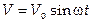 ,
, 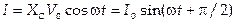 ,
,
где XC = 1/Cω — емкостное сопротивление (ток опережает напряжение на четверть периода)
в) Цепь содержащая индуктивность L:
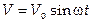 ,
, 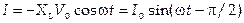 ,
,
где XL = Lω — индуктивное сопротивление (ток отстает от напряжения на четверть периода).
5. Цепь, содержащая R, C и L и источник ЭДС, подчиняющейся закону 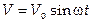 , описывается уравнением:
, описывается уравнением:
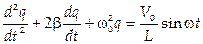 ,
,
где 2β = R/L и 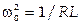 . Решением этого уравнения является выражение
. Решением этого уравнения является выражение 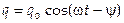 , где
, где
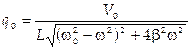 и
и 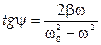 .
.
Амплитуды напряжение на емкости и тока в цепи равны, соответственно:
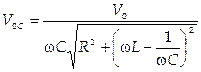 и
и 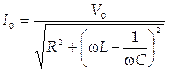 .
.
Тот же результат может быть получен методом векторных диаграмм.
6. Связь между напряжением и током может быть выражена:
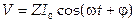 ,
,
где 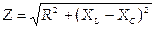 — импенданс и
— импенданс и 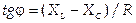 — сдвиг фаз.
— сдвиг фаз.
В цепи наступает резонанс по напряжению на емкости при частоте
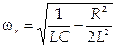 .
.
Резонанс по току наступает при частоте
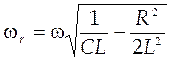
7. Для векторного поля 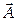 существуют скалярная величина, называемая дивергенцией (div
существуют скалярная величина, называемая дивергенцией (div 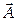 ) и векторная величина, называемая ротором, (rot
) и векторная величина, называемая ротором, (rot 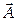 ), равные
), равные
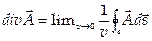 и
и  .
.
8. Используя теоремы Гаусса-Остроградского 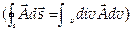 и Стокса
и Стокса 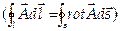 , уравнения Максвелла можно записать в дифференциальном представлении:
, уравнения Максвелла можно записать в дифференциальном представлении:
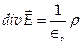
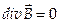
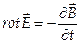
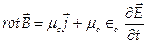 ,
,
где р плотность заряда, и 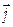 — плотность тока.
— плотность тока.
9. Волновые уравнения для электромагнитной волны при распространении ее в области пространства, не содержащей зарядов и токов:
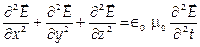 и
и 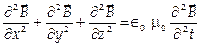
10. Для плоской электромагнитной волны имеем уравнения:
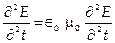 и
и 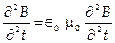 ,
,
решения которых:
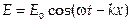 и
и 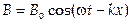 ,
,
где ω — круговая частота волны 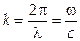 и — волновое число.
и — волновое число.
Величины E и B имеют одинаковые фазы, взаимно перпендикулярны, а амплитуды связаны соотношением 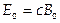 , где c — скорость света.
, где c — скорость света.
11. Экспериментально существование электромагнитных волн было установлено в опытах Г.Герца в 1887 году. А в 1896 году А.С. Попов использовал явление генерации и регистрации электромагнитных волн для передачи информации. Первое сообщение, переданное по радио на расстоянии 250м, было «Генрих Герц».
12. Электромагнитная волна переносит энергию. Плотность энергии в области пространства, где проходит электромагнитная волна равна
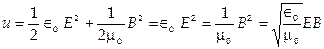
13. Плотность потока энергии определяется вектором Умова-Пойнтинга:
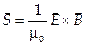 .
.
Дата добавления: 2015-08-08; просмотров: 787;
