Уравнение моментов
Предположим, что точка О неподвижна. В случае одной материальной точки, дифференцируя (3), получаем
.
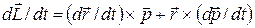При неподвижной точке О вектор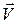 
, равный 
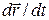, параллелен 
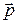и поэтому 
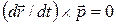. Кроме того 
.
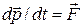Таким образом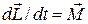 
. (5)
|
Это уравнение моментов для одной материальной точки. Распространим его на систему материальных точек, для чего запишем уравнение (5) для каждой материальной точки механической системы, понимая под М момент всех действующих на нее сил, как внутренних так и внешних. Затем сложим все эти уравнения. Внутренние силы входят в систему попарно так, что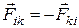 
где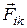 
– сила воздействия k-й материальной точки на i-ю. Кроме того, эти силы 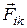и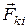 
, действуют вдоль одной и той же прямой. Момент таких двух сил, а значит и моменты всех внутренних сил равны нулю. В результате опять получается уравнение моментов типа (5) только для системы материальных точек, в котором 
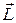определяется выражением (4), а 
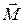– выражением (2) для внешних сил, т. е.
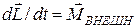. (6)
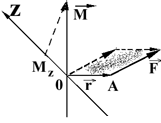
Моментом силы механической системы относительно оси называется проекция на эту ось вектора момента силы системы относительно любой точки, выбранной на рассматриваемой оси (рис. 2). Соответственно, моментом импульса относительно оси называется проекция на эту ось вектора момента импульса относительно любой точки на данной оси.
Можно доказать, что выбор точки на оси влияет на значения моментов импульса 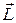и 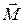относительно точки, но не влияет на значения соответствующих проекций моментов на эту ось.
Если мы выбираем прямоугольную систему координат с началом, совпадающим с полюсом, то имеем:
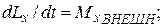
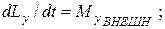
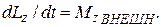(7)
Дата добавления: 2015-08-08; просмотров: 1401;