Момент силы и момент импульса относительно неподвижного начала

Пусть О – какая-либо неподвижная точка в инерциальной системе отсчета. Ее называют началом или полюсом. Обозначим через 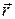радиус-вектор, проведенный из этой точки к точке приложения силы 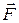(рис. 1) .

Моментом силы 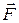относительно точки О называется векторное произведение радиуса-вектора 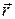на силу 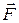: 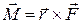, , 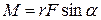(1)

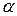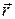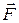– угол между векторами и ;направление 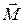выбирается так, чтобы последовательность векторов 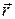, , 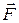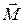образовывала правовинтовую систему, т. е. если смотреть вдоль вектора 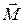, то поворот по кратчайшему пути от первого сомножителя в (1) ко второму осуществлялся по часовой стрелке, таким образом 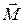совпадает с направлением поступательного движения правого буравчика, рукоятка которого вращается от 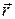к 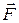по наикратчайшему пути.

Моментом 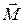нескольких сил относительно точки называется векторная сумма моментов этих сил относительно той же точки

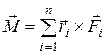. (2)

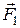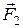Отметим частный случай двух равных параллельных сил и , направленных в противоположные стороны.

Такие силы образуют так называемую пару сил. В этом случае

,

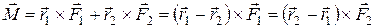т. е. момент пары сил равен моменту одной из этих сил относительно точки приложения другой.

Очевидно, что момент пары сил не зависит от выбора точки О. В частности, если равные и противоположно направленные силы 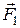и 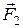действуют вдоль одной и той же прямой, то они коллинеарны с вектором 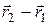, и поэтому момент пары таких сил равен нулю.

Моментом импульса материальной точки относительно точки О называется векторное произведение радиуса-вектора 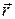на импульс :

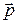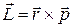. (3)

Для системы n материальных точек моментом импульса относительно некоторой точки О называется векторная сумма моментов импульсов этих точек относительно того же начала:

. (4)