Ускорение
Для характеристики быстроты изменения скорости вводится векторная физическая величина, называемая ускорением 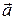 . Она определяется аналогично скорости:
. Она определяется аналогично скорости:
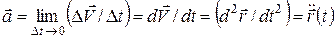 . (10)
. (10)
С учетом формул (7) и (8) из (10) находим
 (11)
(11)
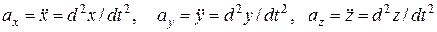 (12)
(12)
– компоненты ускорения, они равны вторым производным соответствующих координат по времени.
С учетом формулы (9) из (10) получаем
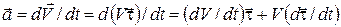 . (13)
. (13)
Можно показать, что
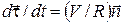 , (14)
, (14)
где R – радиус кривизны в данной точке траектории, а 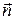 – единичный вектор нормали к траектории в точке, в которой было тело в момент времени t. При этом
– единичный вектор нормали к траектории в точке, в которой было тело в момент времени t. При этом 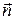 и
и 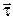 взаимноперпендикулярны (см. рис. 3).
взаимноперпендикулярны (см. рис. 3).
Каждой точке кривой можно сопоставить окружность, которая сливается с траекторией на бесконечно малом ее участке. Радиус этой окружности R., (см. рис. 3), характеризует кривизну линии в рассматриваемой точке и называется радиусом кривизны.
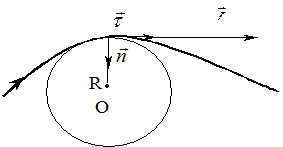 Подставляя (14) в (13), получа
Подставляя (14) в (13), получа 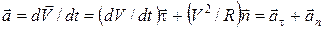 , (15)
, (15)
где
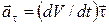 , (16)
, (16)
|
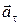 – касательное или тангенциальное ускорение. По величине оно характеризует быстроту изменения модуля скорости:
– касательное или тангенциальное ускорение. По величине оно характеризует быстроту изменения модуля скорости:
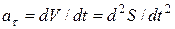 . (17)
. (17)
При ускоренном движении 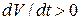 и
и 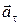 совпадает по направлению со скоростью
совпадает по направлению со скоростью 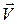 , при замедленном движении
, при замедленном движении 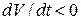 и
и 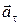 противоположно скорости
противоположно скорости 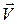 . Второе слагаемое в (15)
. Второе слагаемое в (15)

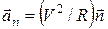 (18)
(18)
|
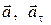 и
и 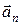 для случая ускоренного движения.
для случая ускоренного движения.
Модуль ускорения точки 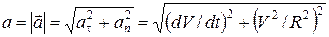 . (19)
. (19)
Ускорение измеряется в метрах на секунду в квадрате (м/с2).
Дата добавления: 2015-08-08; просмотров: 657;
