КИНЕМАТИКА ЭЛЕМЕНТТЕРІ

1. Санақ жүйесі. Траектория. Жол. Орын ауыстыру. Жылдамдық.Қозғалысты түсiндiру үшiн материалдық нүкте деген ұғым енгiземiз.

Материалдық нүкте деп, өлшемі, пішіні оның қозғалысына еш әсерін тигізбейтіндей, массасы бір нүктеге жинақталған денені айтады.

Еркін таңдап алынған макроскопиялық денені немесе денелер жүйесін ойша өзара әсерлесетін бірнеше кішкене бөліктерге бөлеміз де олардың әрқайсысын материалдық нүкте деп қарастырамыз. Сонда еркін таңдап алынған денелер жүйесінің қозғалысын қарастыру материалдық нүктелер жүйесінің қозғалысын қарастыру болып табылады. Механикада алдыменен бір материалдық нүктенің қозғалысы оқытылады, содан кейін материалдық нүктелер жүйесінің қозғалысы оқытылады.

Денелер бір біріне әсер еткенде олар деформацияланады, яғни дене өзінің пішіні мен өлшемдерін өзгертеді. Сол себепті механикада абсолют қатты дене деген ұғым енгізіледі. Абсолют қатты денедеп, қандай жағдай болмасын деформацияға ұшырамайтын және барлық жағдайда да осы дененің екі нүктесінің ара қашықтығы (немесе дәлірек айтқанда екі бөлшектің ара қашықтығы) тұрақты болып қалатын денені айтады.

Қатты дененің кез келген қозғалысын ілгерілемелі және айналмалы қозғалыстар арқылы түсіндіруге болады.

Ілгерілемелі қозғалыста қозғалыстағы қатты денелермен нық байланысқан кез келген түзу өзінің алғашқы жағдайына параллель болып қалады. Немесе барлық нүктелері бір бағытта бірдей жылдамдықпен және үдеумен қозғалады.

Айналмалы қозғалыс дегеніміз дененің барлық нүктелері шеңбер жасап қозғалады және ол шеңберлердің центрлері айналу осі деп аталатын бір түзудің бойында жатады.

Денелердің қозғалысы кеңістікте және уақыт бойынша өтеді. Сол себепті материалдық нүктенің қозғалысын сипаттау үшін осы нүкте кеңістіктің қай жерінде орналасқан және уақыттың қай мезгілінде ол қандай жол жүріп өтті немесе қайда орналасқанын білу керек.

Материалдық нүктенің орны басқа еркін таңдап алынған қандай да–бір басқа денеге қатысты анықталады. Ол дене санақ денесі деп аталады. Онымен байланысқан координаталар жүйесі және санақ денесімен байланысқан сағат жиынтығы-санақ жүйесі деп аталады. Көп қолданылатын декарттық координаталар жүйесінде нүктенің берілген уақыт мезетіндегі орны осы жүйеге қатысты үш координатамен x,y,z немесе радиус-вектормен r сипатталады.

Материалдық нүктенің қозғалысы кезінде оның координатасы уақыт бойынша өзгереді. Жалпы жағдайда оның қозғалысы скаляр теңдеулермен анықталады.

x = x (t)

y = y (t)(1.1)

z = z (t)

Бұл теңдеулер жүйесі келесі векторлық теңдеуге эквивалент болады

r = r(x(t), y(t), z(t)) = r(t) (1.2)

Осы теңдеулер материалдық нүкте қозғалысының кинематикалық теңдеулері деп аталады.

Қозғалыстағы дененің немесе материалдық нүктенің қалдырған ізі–траектория деп аталады. Траекторияның ұзындығын жүрілген жол деп атайды. Белгіленуі-S, өлшем бірлігі-халықаралық бірліктер жүйесінде-метр болады. Дененің бастапқы орны мен соңғы орнын қосатын бағытталған түзу орын ауыстыру деп аталады. Белгіленуі-Dr, векторлық шама, өлшем бірлігі-халықаралық бірліктер жүйесінде метр болады. Траекториясы бойынша қозғалыс түзу сызықты және қисық сызықты болып бөлінеді. Егер траектория түзу болса, қозғалыс түзу сызықты, ал қисық болса. қисық сызықты қозғалыс деп аталды.

Материалдық нүктенің кеңістіктегі орнының өзгеруін сипаттау үшін жылдамдық ұғымын енгіземіз.

Жылдамдық дегеніміз дененің бірлік уақыт ішінде жүрген жолы. Белгіленуі-v, жылдамдық векторлық шама, өлшем бірлігі-халықаралық бірліктер жүйесінде метр/секунда болады.

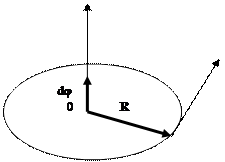
Материалдық нүкте Dt уақыт ішінде М₁ нүктесінен М_2. нүктесіне орын ауыстырсын (1-сурет). Сонда жылдамдық радиус векторының уақыт бойынша бірінші ретті туындысына тең болады. Материалдық нүктенің белгілі бір уақыт аралығында жүрген жолының сол жолға өткен уақытқа қатынасы орташа жылдамдық деп аталады.

V_орт =DS/Dt

Жылдамдық векторы траекторияға жүргізілген жанамамен бағыттас болады. Материалдық нүктенің жылдамдығы Dt уақыт ішінде v₁-ден v₂-ге дейін өзгерген болса, онда жылдамдық өзгерісін келесі түрде Dv=v₂–v₁ жазып, және орташа үдеуді табуға болады.

Бірқалыпсыз қозғалыс кезінде лездік жылдамдықтың модулі уақыт өтуіне қарай өзгереді.

v= limDr/Dt = dr/dt (1.3)

^Dt®0

2. Қисық сызықты қозғалыс. Қисық сызықты немесе шеңбер бойымен қозғалыс кезінде центрге қарай бағытталған үдеу нормаль үдеу деп аталады. Нормаль үдеу жылдамдықтың бағыты жағынан өзгеру шапшаңды-

ғын сипаттайды.

а_n=v²/ r (1.4)

DS

v₁ v₂

В

2-сурет

r₂

а_t

1- cурет а _т

3- сурет

Жанама бойымен бағытталған үдеу тангенциал үдеу деп аталады.

Тангенциал үдеу жылдамдықтың шамасы жағынан өзгеру шапшаңдығын сипаттайды.

а_t=dv/dt (1.5)

Бірқалыпсыз қозғалыс кезінде t дан t+Dt уақыт аралығында жылдамдық өзгерісінің сол өзгеріс болған уақытқа қатынасына тең шама орташа үдеу деп аталады.

а_{ор т}=Dv/Dt (1.6)

Материалдық нүктенің t уақыт мезетіндегі лездік үдеуі орташа үдеудің шегіне тең болады

а_t= lim а_орт = lim(Dv/Dt) = dv/dt (1.7)

^{Dt ® 0 Dt ®0}

Соныменен, үдеу жылдамдықтың уақыт бойынша бірінші ретті туындасы-на тең векторлық шама.

Толық үдеу тангенциал және нормаль құраушылардың (үдеулердің) геометриялық қосындысына тең болады:

а_т = 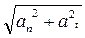(1.8)

Тангенциал және нормаль құраушыларынан тәуелділігіне қарай қозғалыс үдеуін келесі түрде түсіндіруге болады;

1) а_t =0, а_n=0–түзу сызықты бірқалыпты қозғалыс;

2) а_t=а=const, а_n=0–түзу сызықты бірқалыпты айнымалы қозғалыс; Қозғалыстың мұндай түрі үшін келесі өрнекті жазуға болады

а_t =а=Dv/Dt=(v₂–v₁)/(t₂-t₁) (1.9)

Егер бастапқы уақыт мезетінде t₁=0, ал бастапқы жылдамдық v₁=v₀ , онда t₂=t және v₂=v деп белгілеп, a=(v–v₀)/t теңдікті аламыз, осыдан v=v₀ +a t.

Осы формуланы нольден таңдап алынған уақыт мезеті шегінде интегралдап, бірқалыпты айнымалы қозғалыс үшін жүрілген жолды табамыз

S=₀ò ^tvdt=₀ ò ^t (v₀+at)dt= v₀t+at²/2 (1.10)

3) а_t =f (t), a_n=0– айнымалы үдеумен түзу сызықты қозғалыс;

4) а_t=0, а_n=const, а_t=0 болғанда жылдамдық модулі бойынша

өзгермейді, бағыты бойынша өзгереді. a_n=v²/r формуласынан шығатыны қисықтық радиусы тұрақты болу керек. Сондықтан да шеңбер бойымен қозғалыс бірқалыпты болып табылады.

5) а_t =0, а_n ¹0 - бірқалыпты қисық сызықты қозғалыс;

6) а_t = const, а_n ¹ 0 -қисық сызықты бірқалыпты айнымалы қозғалыс;

7) а_t =f (t), а_n ¹ 0 – айнымалы үдеумен қисық сызықты қозғалыс.

Қозғалмайтын ось арқылы айналатын қатты денені қарастырайық. Сонда осы дененің жекелеген нүктелері центрлері айналу осінде жататын, радиустары әртүрлі шеңберлер жасайды.

Дененің айналу бұрышының уақыт бойынша бірінші ретті туындысына тең векторлық шама бұрыштық жылдамдық деп аталады.

w

V

DS

4- сурет. 5- сурет.

w= limDj/Dt = dj/dt (1.11)

^Dt®0

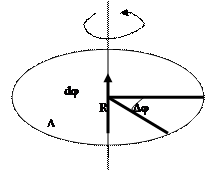
Бұрыштық жылдамдық wвекторы djвекторы сияқты оң бұранда ережесіне сәйкес айналу осі бойымен бағытталған (5-сурет), өлшем бірлігі рад/с.

Нүктенің сызықтық жылдамдығы бұрыштық жылдамдықпен байланысы келесі өрнекпен көрсетіледі: v = wR.

Вектор түрінде жазсақ,

v= [wR] (1.12)

Егер w=const, онда бірқалыпты айналмалы қозғалыс болады және оны айналыс периодымен Т сипаттауға болады. Айналыс периоды дегеніміз- нүктенің толық бір айналысқа кеткен уақыты, яғни 2p бұрышқа бұрылады.

T=2p /w (1.13)

Дененің шеңбер бойымен бірқалыпты айналмалы қозғалысы кезінде бірлік уақыт ішінде жасаған толық айналыс саны айналыс жиілігі деп аталады.

n = 1/T = w /2p осыдан w=2pn .

Бұрыштық жылдамдықтың уақыт бойынша бірінші ретті туындысына тең шама бұрыштық үдеу деп аталады:

e =dw/dt (1.14)

Үдемелі қозғалыс кезінде eвекторы wвекторымен бағыттас болады, кемімелі қозғалыс кезінде оған қарама-қарсы бағытталады.

Тангенциал үдеу a_t = Re. Нормаль үдеу

a_n=v²/R=(w²R²/R)=w² R.

Сонда сызықтық және бұрыштық шамалар арасындағы байланыс келесі өрнектермен жазылады:

S=Rj, v=Rw, a_t=Re, a_n=w² R. (1.15)

Шеңбер бойымен бірқалыпты айнымалы қозғалыс жағдайында (e=const)

w=w₀±et, j=w₀t ±et²/2. (1.16)

Мұндағы w₀ -бастапқы бұрыштық жылдамдық.