Энергия Гельмгольца Изохорно-изотермический потенциал

F = U – TS

Величина (V – TS) является свойством системы; она называется энергией Гельмгольца. Была введена Гельмгольцем в 1882 г.

dF = dU – TdS – SdT,

U = F + TS,

dF = TdS – pdV – SdT,

F – полный дифференциал.

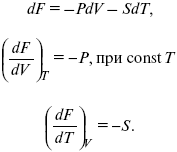
Увеличение объема приводит к тому, что изохорно-изотермический потенциал уменьшается (тот «минус», который стоит перед Р ). Повышение температуры приводит к тому, что F уменьшается.

δА_равн > δА_неравн

Q = ΔU + A,

A = Q – ΔU,

A = T(S₂ – S₁) – (U₂ – U₁),

А = F₁ – F₂ = –ΔF,

А_равн = –ΔF –

физический смысл изохорно-изотермического потенциала.

Убыль изохорно-изотермического потенциала равна максимальной работе, производимой системой в этом процессе; F – критерий направленности самопроизвольного процесса в изолированной системе. Для самопроизвольного процесса: AF_{T г}< 0.

Для несамопроизвольного процесса: ΔF_T,V > 0. Для равновесного процесса: ΔF_T,V = 0.

ΔF_V,T ≤ 0.

Изохорно-изотермический потенциал в самопроизвольных процессах уменьшается и, когда он достигает своего минимального значения, то наступает состояние равновесия (рис. 4).

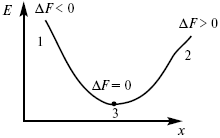
Рис. 4

где 1 – самопроизвольный процесс;

2 – несамопроизвольный процесс;

3 – равновесный процесс.

Изобарно-изотермический потенциал.

1) G (P, Т= cоnst), энергия Гиббса

G = U – TS + PV = H – TS = F + PV,

δQ = dU – Pdv + A′,

δA′ = Q – dU – pdv,

δA′_max = T(S₂ – S₁) – (U₂ – U₁) – p(V₂ – V₁),

δA′_max = (U₁ – TS₁ + PV₁) – (U₂ – TS₂ + PV₂) = G₁ – G₂ = –ΔG,

U – TS + pV = G,

A′_max = –ΔG.

Работа изобарно-изотермического процесса равна убыли изобарно-изотермического потенциала – физический смысл этой функции;

2) функция – полный дифференциал, однозначна, конечна, непрерывна.

G = U – TS + pV,

dG = dU – TdS – SdT + pdv + vdp,

dG = TdS – pdV – TdS – SdT + pdv + vdp,

dG = –SdT + Vdp,

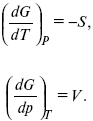
Повышение температуры приводит к тому, что изобарно-изотермический потенциал уменьшается, так как перед S стоит знак «минус». Повышение давления приводит к тому, что изобарно-изотермический потенциал увеличивается, так как перед V стоит знак «плюс»;

3) G как критерий направленности процесса в изолированной системе.

Для самопроизвольного процесса: (ΔG)_P,T < 0. Для несамопроизвольного процесса: (ΔG)_P,T > 0. Для равновесного процесса: (ΔG)_P,T = 0

ΔG_(P,T)≤ 0.

Изобарно-изотермический потенциал в самопроизвольных процессах уменьшается, и, когда он достигает своего минимума, то наступает состояние равновесия.

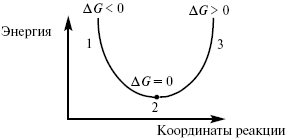
Рис. 5

где 1 – самопроизвольный процесс;

2 – равновесный процесс;

3 – несамопроизвольный процесс.

Совершается работа за счет ΔU и ΔH.

Противодействующие факторы.Энтальпийный фактор характеризует силу притяжения молекул. Энтропийный фактор характеризует стремление к разъединению молекул.

Энтальпия – Н Внутренняя энергия – U.

H = U + PV,

dH = dU + pdv + vdp,

U = TS – PV,

dU = TdS – SdT + pdV + Vdp,

dH = –pdV + pdV + Vdp; U = TdS + VdP.

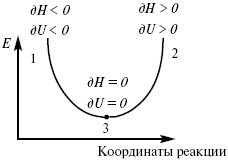
Рис. 6

где 1 – самопроизвольный процесс,

2 – несамопроизвольный процесс,

3 – равновесный процесс,

(dH)_P,T ≤ 0,

(dU)_S,T ≤ 0.

Уравнения Гиббса – Гельмгольца – уравнения максимальной работы.

Они позволяют установить связь между максимальной работой равновесного процесса и теплотой неравновесного процесса

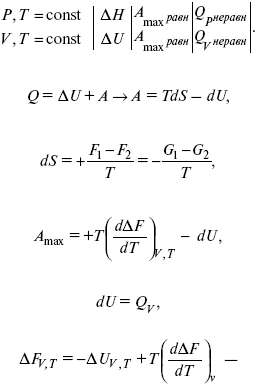
уравнение Гельмгольца (уравнение связывающее функции F и G с их температурными производными).

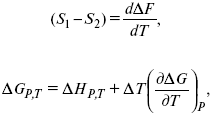
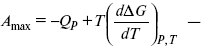
уравнение Гиббса (уравнение связывающее функции F и G с их температурными производными).

Уравнения эти дают возможность рассчитать работу через температурный коэффициент функции Гельмгольца или через температурный коэффициент функции Гиббса.