Системы с эталонными моделями
Эталонные модели в явном или в неявном видах присутствуют во всех адаптивных системах. В качестве эталонных моделей могут быть использованы модели звена, разомкнутой системы, замкнутой системы. Системы, в которых модели присутствуют в явном виде, называются системами с эталонными моделями. Их структуры представлены на рисунке 7.3а, б, где приняты обозначения: Wм – модель замкнутой системы; Wк – корректирующее звено.
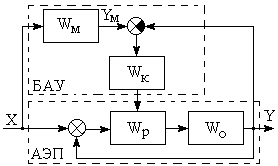  а) б)
Рисунок 7.3
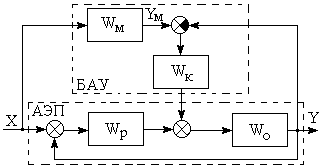
а) б)
Рисунок 7.3
|
Вариант б) – случай адаптивной системы с сигнальной самонастройкой. В случае, когда параметры объекта являются расчетными, фактические и желаемые сигналы будут совпадать, и поэтому сигнал с корректирующего звена равен нулю. При изменении параметров в объекте фактический сигнал будет отличаться от желаемого, что будет приводить к формированию сигнала на выходе корректирующего звена, который, алгебраически суммируясь с сигналом регулятора, формирует такое воздействие на объект, при котором фактический сигнал будет приближаться к желаемому.
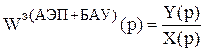 – передаточная функция замкнутой адаптивной системы.
– передаточная функция замкнутой адаптивной системы.
y = [(х-y)Wp + (yм -y)Wк] W0;
yм = XWм;
y= хWpW0 –yWpW0 + xWмWкW0 – yWкW0;
y(1+WpW0 +WкW0) = х(WpW0 +WмWкW0);
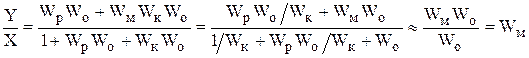 ,
,
Wк = Кк ® ¥.
Передаточная функция такой замкнутой системы независимо от изменения параметров объекта стремится к передаточной функции модели, поэтому переходные процессы по управляющему воздействию Х будут оптимальными и стабилизированными, т.е. не будут изменяться при изменении параметров объекта. Такую сигнальную настройку применяют в системах АВК для сохранения оптимальной настройки в контуре тока при изменении скорости.
Достоинство – простая техническая реализация (пассивный фильтр с операционным усилителем).
Недостатки:
- применяется только для небольших изменений параметров в объекте (20-30-40)%;
- такие системы обеспечивают оптимальность настройки только по задающему сигналу, по возмущающему воздействию система оптимальность не обеспечивает.
Дата добавления: 2015-08-04; просмотров: 864;
