Комплекс ортодонтических мероприятий для профилактики травматических повреждений зубочелюстного аппарата во время занятий спортивными единоборствами.
3.2.1. Анализ напряжённо-деформированного состояния элементной модели зубочелюстного сегмента в участке медиального резца верхней челюсти.
Предварительно был проанализирован общий ЭМ ЗЧС при действии статических нагрузок, близких к функциональным. Сила прикладывалась в участке язычной поверхности выше режущего края на одну треть коронки и равнялась 100н, то есть силе, возникающей во время жевания твердой еды в участке резцов.
Обнаруженные суммарные перемещения зуба равнялись 0,908 мм (горизонтальные 0,888, а вертикальные 0,297мм), малая степень подвижности зуба не превышала физиологическую норму [106]. Полученные результаты свидетельствуют, что построенная модель и все ее параметры отвечают здоровому зубу человека.
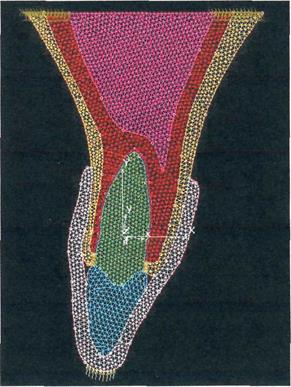
Рисунок 3.2.1.1. ЭМ ЗЧС с каппой.
Так как, в контактных видах спорта зуб, в основном, поддается импульсным, динамическим нагрузкам, был проведён частотный анализ собственных колебаний системы (с помощью специальной программы в программном пакете Сosmos) (Рис. 3.2.1.1). При этом обнаружен факт, что ЗЧС является высокочастотной структурой, у которой спектр частот собственных колебаний начинается с частоты около 2000 Гц.
Присоединение каппы снижает частоту первого тона колебаний, но и при этом период колебаний значительно меньше, чем длительность импульса удара спортсмена.
Так как модель ЗЧС с каппой вышла достаточно сложной, для уточнения ясности предполагаемого анализа, считаем целесообразным предварительно изложить некоторые основные понятия сопротивления материалов для случая, когда зуб или ЗЧС, в первом приближении, может быть представлен в виде консольно - закрепленной балки, с постоянным по длине поперечным сечением (Рис. 3.2.1.2).
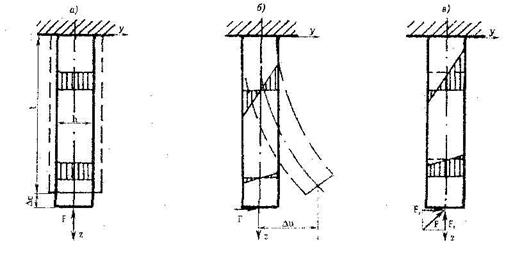
Рисунок 3.2.1.2. Напряженно-деформированное состояние "зуба-балки".
При действии поперечной силы "балка" - ЗЧС начинает сгибаться (в). При общем действии вертикальной и горизонтальной составной силы напряжения складывается алгебраизм (с учетом знака).
Для обеспечения сравнений полученных результатов, будем принимать силу F = 100 Н. Моделирование влияния удара на каппу осуществлялось путем распределения сосредоточенной силы на 9 узлов симметрично среднего узла по закону косинуса.
Таблица 3.2.1.1
Результаты НДС ЭМ ЗЧС
| № α, град. «К» / «М» | Перемещение, Di - 103, м | Напряжение,σi ·10¯6, Па | ||||||
| Dr | Режущий край зуба | Зуб | Компактная кость | Перио-донт | ||||
| Dх | Dy | σм | σy | σм | σy | σy | ||
| 1.α =0 | 0,03 | -0,0143 | 0,027 | 20,39 | -27,4 | 6,0 | -6,5...2,64 | -1,42 |
| 2. α =0 «К» | 1,118 | -0,017 | 0,028 | 6,89 | -8,34 | 6,03 | -7,24...2,84 | -1,35 |
| З. α =0 «М» | 0,033 | -0,01 | 0,024 | 6,7 | -7,68 | 6,1 | -6,6...3,61 | -1,2 |
| 4. α =60 «К» | 1,125 | 0,428 | -0,064 | 11,9 | -13,9 | 23,96 | -26,6...24,2 | -0,312 |
| 5. α =60 «М» | 0,34 | 0,313 | -0,044 | 8,96 | -9,79 | 23,88 | -26,74...23,7 | -0,335 |
| 6. α =60 «М» | 0,33 | 0,301 | -0,041 | 6,2 | -7,78 | 23,5 | -26,3...23,3 | -0,397 |
В первом столбике таблицы наводится номер расчетного случая, угол действия силы относительно продольной оси зуба в градусах, механические свойства материала каппы «К» - модуль упругости материала близок к каучуку, «М» - модуль упругости близок к виниловым пластинкам. В следующих колонках таблицы наводятся наиболее характерные значения напряжений и перемещений, которые предусматривается использовать для анализа.
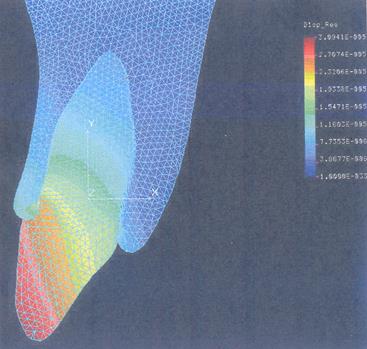
Рисунок 3.2.1.3. Поле суммарных перемещений при действии нагрузка вдоль продольной оси зуба.
Отметим, что перемещения Пк (вторая колонка таблицы) отображают максимальные перемещения в системе - это перемещение точки каппы, где прилагается максимальная нагрузка. В первом расчетном случае они представляют собой геометрическую сумму перемещений режущего края зуба Dх и Dу. Приведенные в таблице значения перемещений для наиболее характерной точки зуба - режущего края, позволят побочно оценивать характер деформации всего ЗЧС.
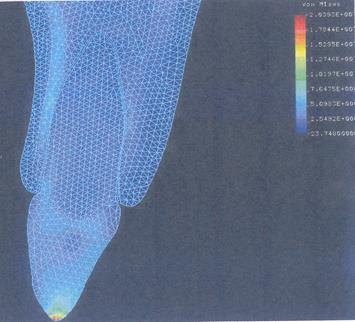
Рисунок 3.2.1.4. Поле эквивалентных напряжений при действии нагрузка вдоль продольной оси зуба.

Рисунок 3.2.1.5. Поле суммарных перемещений при действии нагрузки вдоль продольной оси зуба и каппы из материала "К".
Программа, с помощью которой построена и анализируется модель, записывает решение задачи перемещения каждого узла по трем координатам, напряжения нормальные и касательные и напряжения по Мизесу в каждой узловой точке и в середине каждого элемента.
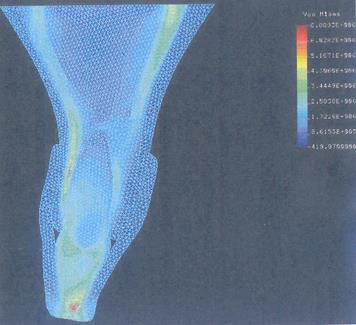
Рисунок 3.2.1.6. Поле эквивалентных напряжений при действии нагрузки вдоль продольной оси зуба и каппы из материала "К".
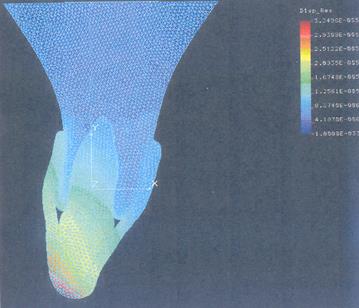
Рисунок 3.2.1.7. Поле суммарных перемещений при действии нагрузки вдоль продольной оси зуба и каппы из материала "М".
Результаты могут трактоваться как базовые. Поле суммарных перемещений показано на рис. 4.3, а поле напряжений по Мизесу - на рис. 3.2.1.4.
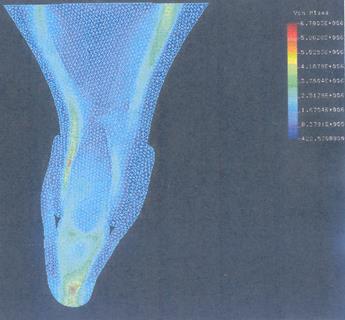
Рис. 3.2.1.8. Поле эквивалентных напряжений при действии нагрузки вдоль продольной оси зуба и каппы из материала "М".
Вторая и третья строки таблицы отображают ЭМ ЗЧС при действии нагрузки вдоль продольной оси зуба (то есть при нанесении удара по нижней челюсти снизу, и зубы - антагонисты ударяются друг в друга). Наличие каппы привело к уменьшению максимальных напряжений в зубе в три раза.
Напряжение в стенках альвеолы небольшие, сжимается как губная так и язычная стенки (Рис. 3.2.1.2), однако из-за несимметрии структуры ЗЧС поддается небольшому изгибу, что видно из разницы сжимающих напряжений в левой и правий частях альвеолы (Рис. 3.2.1.5; 3.2.1.6; 3.2.1.7; 3.2.1.8).
Особенное внимание следует обратить на последнюю колонку таблицы, в которой приводятся значения осевых вертикальных напряжений в слоях периодонта, расположенных у корня зуба. С одной стороны, эти напряжения небольшие, однако уже при значении силы, отвечающей максимальной виносливости для резца по Габеру - 250н, их следует увеличить в 2,5 раза.
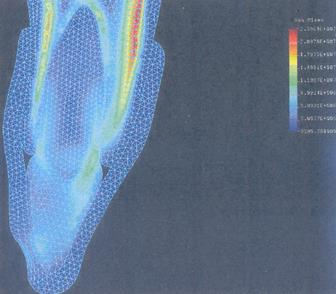
Рисунок 3.2.1.9. Поле эквивалентных напруг при действии внешней силы под углом и каппы из материала "К".
В этом случае величина действующих напруг будет лежать в пределах 3,0 - 3,55 Мпа, то есть в пределах разрушительных напряжений для периодонта (Табл. 3.2.1.1).
В четвертой и пятой строках приводятся основные результаты анализа ЭМ ЗЧС, защищенного ЗДК при нанесении прямого удара, сила действует на зуб под углом близким 60° относительно продольной оси зуба (Рис. 3.2.1.9; 3.2.1.10).
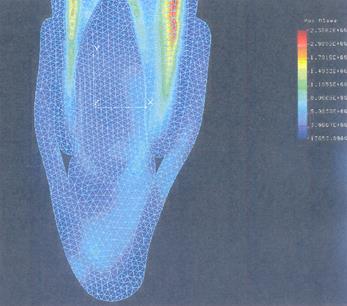
Рисунок 3.2.1.10. Поле эквивалентных напряжений при действии внешней силы под углом и каппы из материала "М".
В последней шестой строке приводятся результаты анализа модели из ЗНЯК, толщина увеличилась в 1,5 разы и равняется Змм (Рис. 3.2.1.11).
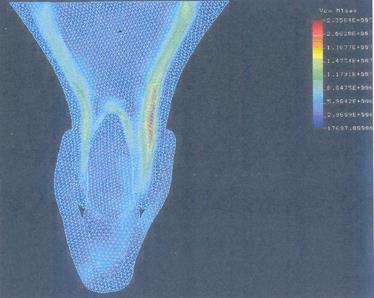
Рисунок 3.2.1.11. Поле эквивалентных напряжений при действии внешней силы под углом из материала "М" увеличенной толщины.
Исследование ЭМ ЗЧС в каждом конкретном случае плоской или объемной позволяет прогнозировать возможные травматические повреждения зубочелюстного комплекса у конткретного спортсмена, анализировать защитные свойства ЗДК.
Дата добавления: 2015-08-04; просмотров: 1332;
