Электромагнитные волны. Свойства электромагнитных волн

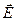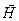В прошлом семестре, завершая рассмотрение системы уравнений классической электродинамики Максвелла, мы установили, что совместное решение двух последних уравнений (о циркуляции векторов и ) приводит к дифференциальному волновому уравнению.

Так мы получили волновое уравнение «Y» волны:

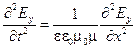. (3.6)

Электрическая компонента y – волны распространяется в положительном направлении оси X с фазовой скоростью

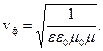(3.7)

Аналогичное уравнение описывает изменение в пространстве и во времени магнитного поля y – волны:

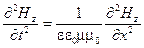. (3.8)

Анализируя полученные результаты, можно сформулировать ряд свойств, присущих электромагнитным волнам.

1. Плоская «y» - волна является линейно поляризованной поперечной волной. Векторы напряженности электрического ( 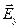), магнитного ( 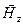) поля и фазовой скорости волны ( ) взаимно перпендикулярны и образуют «правовинтовую» систему (рис.3.1).

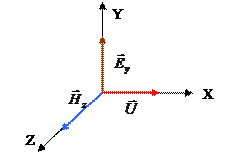
Рис.3.1

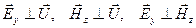
2. В каждой точке пространства компонента волны H_z пропорциональна напряженности электрического поля E_y:

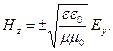
Здесь знаку «+» соответствует волна, распространяющаяся в положительном направлении оси X. Знак «-» — в отрицательном.

3. Электромагнитная волна движется вдоль оси X с фазовой скоростью

Здесь .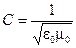

При распространении электромагнитной волны в вакууме (ε = 1, μ = 1) фазовая скорость

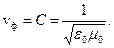
Здесь электрическая постоянная ε₀ = 8.85 · 10^-12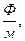

магнитная постоянная μ₀ = 4π · 10^-7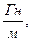

.

.

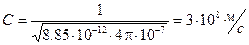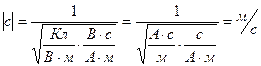Совпадение скорости электромагнитной волны в вакууме со скоростью света стало первым доказательством электромагнитной природы света.

В вакууме упрощается связь напряженности магнитного и электрического полей в волне.

.

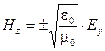При распространении электромагнитной волны в диэлектрической среде (μ = 1) 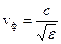и .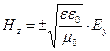

3. Энергетические характеристики электромагнитных волн.
Вектор Пойнтинга

Сегодня нет надобности доказывать, что распространяющаяся электромагнитная волна обладает энергией. Достаточно напомнить, что жизнь на Земле обеспечивается энергией солнечного света, то есть электромагнитной волны.

В 1901 году русский ученый А. С. Попов создал аппаратуру, позволившую установить радиосвязь на расстоянии 150 км. А уже на следующий год итальянский инженер Г. Маркони, используя энергию электромагнитных волн, осуществил радиотелеграфную передачу через Атлантический океан.

Как же вычислить энергию электромагнитной волны? Для определенности рассмотрим плоскую, гармоническую, монохроматическую «y» — волну в вакууме.

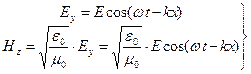(3.9)

Волна, представляющая собой комбинацию электрического и магнитного полей, будет обладать энергией, равной сумме энергий этих полей.

Плотность энергии электрического поля:

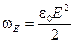. (3.10)

Плотность энергии магнитного поля:

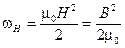. (3.11)

Таким образом, объемная плотность полной энергии электромагнитной волны

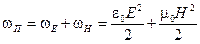. (3.12)

Воспользовавшись уравнениями (3.9), представим эту плотность энергии волны в виде:

.

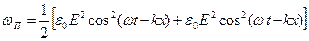Объемная плотность энергии электромагнитной волны меняется пропорционально квадрату амплитуды электрического вектора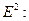

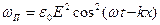. (3.13)

Так же как и в случае упругой волны, введем энергетическую характеристику электромагнитной волны — интенсивность.

Интенсивность определим величиной энергии, которая ежесекундно протекает вместе с волной (со скоростью с) через поверхность единичной площадки, перпендикулярной к направлению распространению волны.

. (3.14)

Преобразуем это выражение интенсивности, вспомнив, что скорость света в вакууме

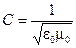
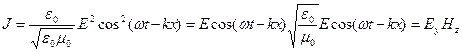(3.15)

Произведение напряженностей (E_y H_z) можно рассматривать, как модуль векторного произведения 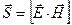(напомним, что в волне ).

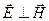Это векторное произведение будет определять уже не скалярную характеристику волны – интенсивность (J), а векторную ( 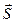). Этот вектор получит название вектора Пойнтинга.

Модуль вектора Пойнтинга равен интенсивности волны

.

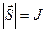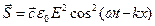Направление вектора Пойнтинга ( 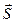) — вектора плотности потока энергии электромагнитной волны – совпадает с направлением её фазовой скорости. В нашем частном случае :

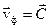Интенсивность волны пропорциональна квадрату амплитуды (Е²) вектора E_y и пульсирует по закону квадрата косинуса (см.3.15). Легко отыскать среднее значение этой величины, если вспомнить, что .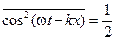

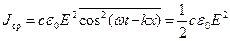(3.16)