Особенности упругого подвеса и упругих элементов.

(вернуться к оглавлению)

Упругие подвесы и элементы имеют определенные преимущества в сравнении с контактными опорами. Прежде всего, из-за того, что в них исключены силы и моменты сухого трения.

Но в них наблюдаются свои специфические дестабилизирующие факторы. В частности, из-за наличия внутреннего трения в материале подвесов. Для прецизионных приборов приходится это иметь в виду из-за появления дополнительных источников погрешностей. Неоднозначности статической характеристики при знакопеременной нагрузке и нестабильности показаний во времени при стабильном внешнем воздействии.

В зависимости от условий эксплуатации эти дополнительные погрешности определяют как гистерезис характеристики, упругое последействие первого и второго рода, релаксацию напряжения, внутреннее трение. Это происходит при любых минимальных нагрузках, не превосходящих пределов пропорциональности (см. рисунок)

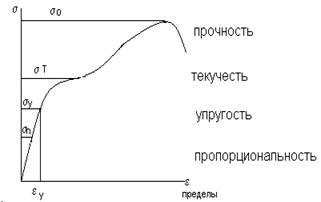
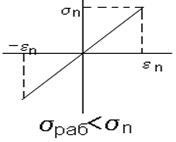
Рис. Диаграмма напряжение σ – относительная деформация ε

На диаграмме отмечены характерные области.

σ_п- максимальное напряжение, при котором наблюдается линейная зависимость σ от 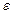. Это зона пропорциональности. Приборные упругие элементы должны иметь нагрузки, не превосходящие этой области (См. рис. справа).;

σ_у – предел упругости. Это максимальное напряжение, при котором сохраняется взаимно однозначное соответствие между σ и 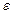с наперед заданной погрешностью, при заметной нелинейности.

σ_т , σ_b – соответственно, предел текучести и предел прочности.

Рассмотрим участок диаграммы напряжение – деформации в пределах зоны пропорциональности в измененном масштабе и размерностях по осям. Это придаст большую наглядность тому, что происходит в реальном приборе, в частности, в осевом акселерометре.

По вертикальной оси отложена упругая деформация провеса по оси измерения, пусть, - y или позиционная сила – С_yy.

По горизонтальной оси – измеряемое ускорение - a_y или инерционная сила - Ma_y.

Ma_y=Cy - условие статического равновесия a_y=Cy/M – калибровочная характеристика акселерометра при наличие упругого подвеса . В идеальном случае она линейна. Но реально при знакопеременной нагрузке появляется петля гистерезиса, площадь которой характеризует энергию рассеивания (диссипацию энергии за счет сил внутреннего трения) в материале упругой системы.

Рис. Диаграмма напряжения.

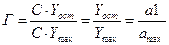- характеристика гистерезиса, относительная величина.

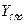-остаточная деформация, когда после возрастания нагрузка снизилась до нуля.

Оценим численные значения гистерезиса характеристики для наиболее стабильных в этом смысле материалов.

С - таль, бронза, латунь Г_ср=10^-3 -5*10^-4 ;

Специальные сплавы - PtAg, K40HXMB, MP-40, MPB Г=10^-4 - 5*10^-5

Наилучшими показателями по этому параметру обладает кварцевое стекло - двуокись кремния SiO₂ или кристаллический кварц.

Г_кварц/Г_металл<10^-3 – 10^-5

Упругое последействие (УП) это самопроизвольное изменение деформации упругой деформации после прекращения изменения внешних сил или моментов сил.

УП₁ - упругое последействие первого рода – после нагрузки. Оно проявляется в увеличении деформации при постоянстве внешней силы.

УП₂ - упругое последействие второго рода – после разгрузки. Проявляется в уменьшении деформации при постоянстве внешней силы

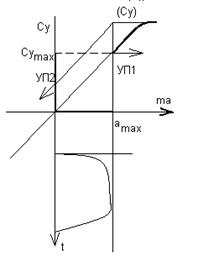^{(Рис. дораб. пояснения}[G9] ⁾

Рис. Диаграмма упругого последействия.