Подвесы в виде балок. (вернуться к оглавлению)
Довольно обширный класс электромеханических преобразователей использует в качестве элементов подвеса консольные балки с различной конфигурацией поперечного сечения.
Если это акселерометр, то рисунок иллюстрирует кинематику и характер нагружения такого стержня распределенными и сосредоточенными силовыми факторами.

Рис.Кинематика и Схема нагружения балочного подвеса
Будем использовать метод сечений. Балка консольно закреплена, имеет собственную распределенную по длине массу и сосредоточенную на свободном конце массу М.
Они дают соответственно сосредоточенную силу 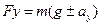 , и распределенную нагрузку на единицу длины -
, и распределенную нагрузку на единицу длины - 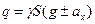 .
.
Здесь 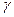 - плотность материала стержня[кг/м3], S-площадь его поперечного сечения
- плотность материала стержня[кг/м3], S-площадь его поперечного сечения
В зависимости от конфигурации поперечного сечения балки такой подвес может обеспечивать преимущественные степени свободы по осям Y и Z (прогиб - y(x, ay)), z(x, az)) и углы поворота соответствующих сечений -
Необходимо получить
(1) 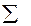 Fy=0è
Fy=0è 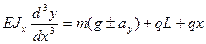
- уравнение равновесия сил;
(2) 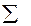 Mx=0è
Mx=0è 
- уравнение равновесия моментов;
(3) 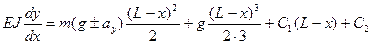
-уравнение углов поворота в сечении;
(4) 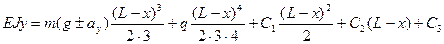
-уравнение прогиба;
 C1, C2, C3 : x=0 ; y=0
C1, C2, C3 : x=0 ; y=0
x=0 ; 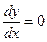 |è x=L ;
|è x=L ; 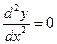

1) 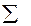 Fx=0
Fx=0
2) 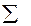 Mx=0
Mx=0
3) dy/dx(x)
4) J(x)
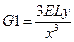
(рис. Доработать)[G8]
E-модуль упругости первого рода
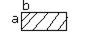
J-статический момент инерции
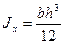 - изгиб от нагрузки по оси y
- изгиб от нагрузки по оси y
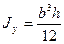
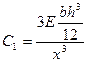
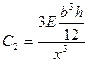
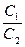 —степень неравножесткости системы
—степень неравножесткости системы
 А значит , чтобы система была равножесткой , должно выполняться условие: C1=C2
А значит , чтобы система была равножесткой , должно выполняться условие: C1=C2
Упругий элемент рассматривается как некоторый подвес, обеспечивающий нужные степени свободы, одновременно он выполнял роль упругого элемента, т.к. он обладает конечной жесткостью С.
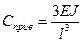 - жесткость, приведенная к точке x=L
- жесткость, приведенная к точке x=L
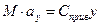
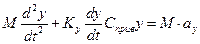
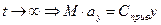
Дата добавления: 2015-08-04; просмотров: 929;
