Модель транзистора для большого сигнала (модель Эберса-Молла).

В качестве такой модели наибольшее распространение получила модель Эберса-Молла, которая основывается на уравнении диода (уравнении Шокли). Эта модель при достаточно высокой точности является наименее сложной (содержит минимальное количество элементов с легко измеряемыми параметрами).

Общая эквивалентная схема транзистора, используемая при получении математической модели Эберса-Молла, показана на писунке.

Каждый переход транзистора p-n-p типа представлен в виде диода, а их взаимодействие отражено генераторами токов, где:

α_I – инверсный коэффициент передачи тока (из коллектора в эмиттер);

α_N – нормальный коэффициент передачи тока (из эмиттера в коллектор)

α_NI₁ – генератор коллекторного тока при нормальном включении;

α_II₂ – генератор эмиттерного тока при инверсном включении.

Таким образом, токи эмиттера и коллектора в общем случае содержат две составляющие: инжектируемую (α_I или α_N) и экстрактируемую (α_NI₁или

α_II₂), поэтому:

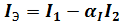; (1)

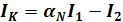(2)

Если в общей эквивалентной схеме поочередно прикладывать напряжение к каждому p-n переходу, а выводы других, соответственно, поочередно замыкать между собой накоротко, то токи I₁и I₂, протекающие через p-n переходы к которым приложено напряжение (в соответствии с уревнением Шокли) примут вид:

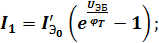(3)

(4)

где 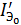- тепловой ток эмиттерного p-n перехода при замкнутых базе и коллекторе;

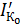- тепловой ток коллекторного p-n перехода при замкнутых базе и эмиттере.

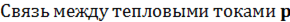−n переходов 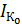, , 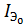включенных раздельно и тепловыми токами 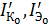получим из (1) и (2).

Пусть 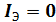,тогда .

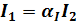При .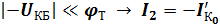

Подставив эти выражения в (1) и (2) для тока коллектора получим:

,

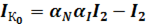учитывая, что 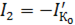имеем:

,

;

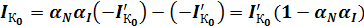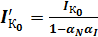Аналогично: .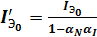

Токи коллектора и эмиттера с учетом (3) и (4) будут:

;

;

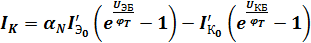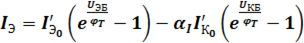На основании закона Кирхгофа ток базы будет: ;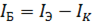

.

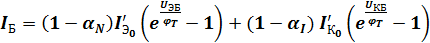В самом общем случае в транзисторах справедливо равенство:

,

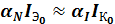тогда при ,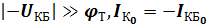

поэтому

.

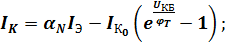
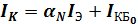Последние уравнения описывают выходные ВАХ транзистора.

Из уравнения для определения I_Э, решенное относительно U_ЭБ, получим выражение для идеализированных входных характеристик транзистора:

.

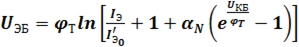Учитывая, что обычно 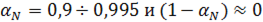, последнее уравнение может быть упрощено:

.

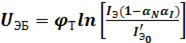Модели Эберса-Молла, несмотря на их приближенность, очень полезны для анализа статических режимов при больших изменениях сигналов, так как они нелинейные.