Графический метод (метод энергии)
Расчёт производится с использованием уравнения удельной энергии сечения:
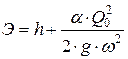 , (П.5.1)
, (П.5.1)
где h – глубина, м; a – коэффициент Кориолиса; Q – расход в русле (канале), м3/с; g – ускорение свободного падения, м/с2; w – площадь живого сечения, м2.
Порядок расчёта:
1. Задаваясь произвольно выбранными значениями глубин определяют значение энергии для каждой заданной глубины.
2. По вычисленным данным строят график зависимости 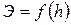 . На построенном графике на оси Э минимальному значению энергии будет соответствовать критическая глубина.
. На построенном графике на оси Э минимальному значению энергии будет соответствовать критическая глубина.
3. Расчёт удобно представлять в табличном виде (табл. П.5.1).
Таблица П.5.1
| h, м | 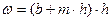 , м , м
| 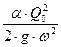 , м , м
| Э, м |
| h1 | w1 | … | Э1 |
| h2 | w2 | … | Э2 |
| h… | w… | … | Э… |
| hn | wn | … | Эn |
Пример вычисления. Дано: расход Q = 12 м3/с, ширина канала понизу b = 3 м, m = 2. Необходимо найти критическую глубину hк.
Решение. Зададимся значениями глубин и определим площадь живого сечения по формуле (2). Расчёт сведём в таблицу (табл. П.5.2).
Таблица П.5.2
| h, м | 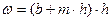 , м , м
| 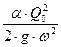 , м , м
| Э, м |
| 0,90 | 4,32 | 0,4326 | 1,3326 |
| 0,91 | 4,39 | 0,4196 | 1,3296 |
| 0,92 | 4,45 | 0,4072 | 1,3272 |
| 0,93 | 4,52 | 0,3952 | 1,3252 |
| 0,94 | 4,59 | 0,3837 | 1,3237 |
| 0,95 | 4,66 | 0,3726 | 1,3226 |
| 0,96 | 4,72 | 0,3619 | 1,3219 |
| 0,97 | 4,79 | 0,3516 | 1,3216 |
| 0,98 | 4,86 | 0,3417 | 1,3217 |
| 0,99 | 4,93 | 0,3321 | 1,3221 |
| 1,00 | 5,00 | 0,3229 | 1,3229 |
По полученным данным строим график зависимости 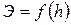 .
.
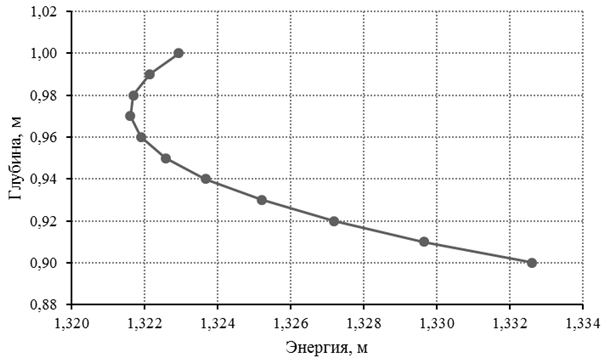
Рис. П.5.1. График зависимости удельной энергии Э сечения от глубины
На полученном графике на оси Э минимальному значению энергии соответствует критическая глубина 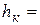 0,97 м.
0,97 м.
Дата добавления: 2015-07-07; просмотров: 932;
