Определение критического уклона
Для определения критического уклона на быстротоке можно воспользоваться любой известной формулой (п. 3.1.3.).
Для вывода о состоянии потока необходимо проанализировать соотношение нормальной глубины 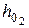 и критической глубины
и критической глубины 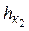 на водоскате быстротока. Для правильности вывода проверить соотношение заданного уклона дна русла
на водоскате быстротока. Для правильности вывода проверить соотношение заданного уклона дна русла 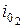 и вычисленного критического уклона
и вычисленного критического уклона 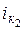 .
.
Сравнивая нормальную глубину с критической, необходимо назначить глубину на изломе дна подводящего канала и быстротока.
3.2.4. Расчёт кривой свободной поверхности на быстротоке
Продольный профиль поверхности потока воды называется кривой свободной поверхности [17, 19].
В призматических руслах для описания изменения глубины h по длине потока l при неравномерном движении используется следующее дифференциальное уравнение:
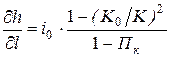 , (25)
, (25)
где 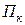 – параметр кинетичности. Расчёт сводится к интегрированию данного уравнения.
– параметр кинетичности. Расчёт сводится к интегрированию данного уравнения.
Увеличение глубины воды в сторону течения называется подпором, а свободная поверхность при этом – кривая подпора. При убывании глубины свободная поверхность образует кривую спада. К линии нормальных глубин N–N кривая свободной поверхности всегда приближается асимптотически, а к линии критических глубин K-K – резко, под углом 90°.
Существует несколько методов расчёта кривой свободной поверхности: Б.А. Бахметева, метод акад. Н.Н. Павловского и другие. В практике дорожно-мостового и аэродромного строительства приходится решать задачи по расчёту неравномерного плавноизменяющегося движения воды не только в призматических руслах, но и на непризматических участках каналов. Поэтому предлагается студентам воспользоваться универсальным методом конечных разностей, предложенным В.И. Чарномским.
Метод В.И. Чарномского заключается в следующем: зная глубину в одном из сечений канала, например глубину на изломе дна подводящего канала и лотка быстротока 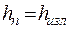 , задаёмся значением глубины в соседнем сечении
, задаёмся значением глубины в соседнем сечении 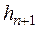 и находим искомое расстояние
и находим искомое расстояние 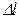 между двумя соседними сечениями с известными глубинами по уравнению
между двумя соседними сечениями с известными глубинами по уравнению
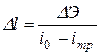 , (24)
, (24)
где 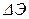 – изменение удельной энергии сечения в пределах выбранного участка;
– изменение удельной энергии сечения в пределах выбранного участка; 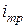 – уклон трения (среднее значение гидравлического уклона в пределах рассматриваемого участка).
– уклон трения (среднее значение гидравлического уклона в пределах рассматриваемого участка).
Для удобства расчёт сводится в табл. 7.
Сложность заполнения таблицы заключается в том, что определяемые величины подразделяются на построчные и междустрочные. В табл. 7 знаком "–" указано место положения определяемой величины. Так, построчными значениями являются w, c, R, …, соответствующие назначенной глубине 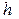 , а междустрочными –
, а междустрочными – 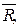
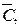 …., определяемые как среднеарифметические или по соответствующим формулам.
…., определяемые как среднеарифметические или по соответствующим формулам.
Приведём необходимые для расчёта понятия и формулы с нумерацией по столбцам:
1) 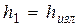 ;
; 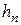 – последняя глубина на быстротоке принимается на 2 % больше нормальной глубины, т.е.
– последняя глубина на быстротоке принимается на 2 % больше нормальной глубины, т.е. 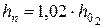 ; промежуточные глубины рекомендуется задавать с интервалом 0,1 м, опираясь на удобные при последующем построении числовые значения глубин (например,
; промежуточные глубины рекомендуется задавать с интервалом 0,1 м, опираясь на удобные при последующем построении числовые значения глубин (например, 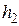 =1,1; 1,0: 0,9;…);
=1,1; 1,0: 0,9;…);
Таблица 7
Расчёт длины кривой свободной поверхности на водоскате быстротока
| h |
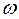
|

|
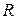
| _
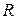
|
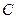
| _
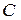
|
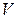
| _
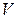
|
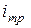
|
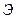
|
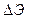
|
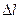
|
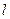
|
| h1 | – | – | – | – | – | – | |||||||
| – | – | – | – | – | – | ||||||||
| h2 | – | – | – | – | – | – | – | ||||||
| – | – | – | – | – | – | ||||||||
| h3 | – | – | – | – | – | – | – | ||||||
| … … … … | |||||||||||||
| hп | – | – | – | – | – | – | – |
2) 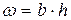 , т.к. лоток прямоугольной формы и коэффициент откоса
, т.к. лоток прямоугольной формы и коэффициент откоса 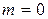 ;
;
3)  , т.к. лоток прямоугольной формы и коэффициент откоса
, т.к. лоток прямоугольной формы и коэффициент откоса 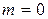 ;
;
4) 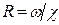 ;
;
5) 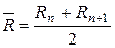 , где
, где 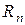 и
и 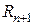 – гидравлические радиусы, соответствующие соседним глубинам;
– гидравлические радиусы, соответствующие соседним глубинам;
6) 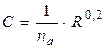 , где
, где 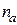 – коэффициент шероховатости с учётом аэрации потока;
– коэффициент шероховатости с учётом аэрации потока;
7) 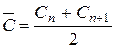 , где
, где 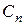 и
и 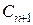 – коэффициенты Шези, соответствующие соседним глубинам;
– коэффициенты Шези, соответствующие соседним глубинам;
8) 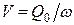 , где
, где 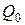 – заданный расход воды, поступающий из подводящего канала;
– заданный расход воды, поступающий из подводящего канала;
9) 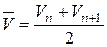 , где
, где 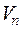 и
и 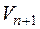 – средние скорости в соседних сечениях;
– средние скорости в соседних сечениях;
10) 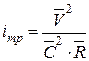 ;
;
11) 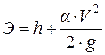 , где
, где 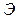 – удельная энергия соответствующих сечений;
– удельная энергия соответствующих сечений;
12) 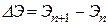 , где
, где 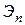 и
и 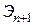 – удельные энергии соседних сечений, причём в последующем сечении для данного типа кривой спада удельная энергия сечения больше, чем в предыдущем;
– удельные энергии соседних сечений, причём в последующем сечении для данного типа кривой спада удельная энергия сечения больше, чем в предыдущем;
13) 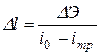 ;
;
14) 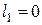 , т.к. расчёт кривой свободной поверхности начинается с точки излома дна; последующие числовые значения длин
, т.к. расчёт кривой свободной поверхности начинается с точки излома дна; последующие числовые значения длин
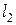 ,
, 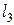 , … определяются путём наращивания, а именно:
, … определяются путём наращивания, а именно: 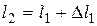 ,
, 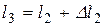 и т.д.
и т.д.
Назначение глубин для расчёта кривой свободной поверхности будет правильным, если при вычислении приращения длины 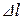 (столбец 13 в табл. 7) не появятся отрицательные значения.
(столбец 13 в табл. 7) не появятся отрицательные значения.
3.2.5. Построение кривой свободной поверхности
на водоскате быстротока
Построение кривой свободной поверхности выполняется на миллиметровой бумаге формата А4 или А3 в следующих масштабах: вертикальный – 1:10, горизонтальный – свободный стандартный, но предполагающий достаточную точность (1,0 м) при определении длины участка при соответствующей глубине (1:100, 1:200, …).
Кривая свободной поверхности строится в виде графика с вертикальной осью глубин и горизонтальной осью длин (рис. 11).
На графике обязательно указываются линии критических К–К и нормальных N–N глубин. Отдельные значения глубин и длин по осям отмечать не следует, чтобы не загромождать график. Для построения кривой свободной поверхности точки на графике соединять плавно по лекалам.
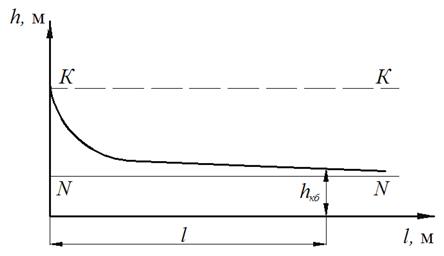
Рис. 11. Пример построения графика кривой
свободной поверхности
Используя график свободной поверхности необходимо принять глубину в конце быстротока.
В большинстве случаев длины призматических русел бывают достаточными, чтобы на них успевал устанавливаться равномерный режим и отвечающая ему нормальная глубина потока h0. Для назначения требуемой глубины (в курсовой работе длина быстротока l – величина заданная) придерживаются следующих условий:
– если длина быстротока равна или больше длины кривой спада, то глубину на конце быстротока принимают равной нормальной глубине 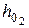 ;
;
– если же, наоборот, длина кривой спада будет больше длины быстротока, то глубина на конце быстротока определяется по графику: на горизонтальной оси длин откладывается значение длины быстротока (см. п. 2.2), поднимается вертикаль до пересечения с кривой, слева на вертикальной оси глубин снимается значение 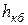 .
.
Дата добавления: 2015-07-07; просмотров: 1797;
