Пример расчета средней гармонической взвешенной
Трудоемкость продукции ( 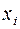 ),
ч ),
ч
| Трудоемкость
по группе ( 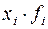 ),
Чел.-ч. ),
Чел.-ч.
| 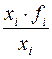
|
| 0,90 | 4,50 | |
| 0,95 | 6,65 | |
| 1,01 | 10,10 | |
| 1,20 | 6,00 | |
| 1,25 | 3,75 | |
| ИТОГО | 31,00 |
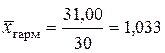 чел. - ч.
чел. - ч.
Средняя квадратическая применяется только тогда, когда варианты представляют собой отклонения фактических величин от их средней арифметической или от заданной нормы.
Средняя квадратическая может быть простой и взвешенной и определяется соответственно по формулам:
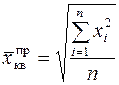 ,
, 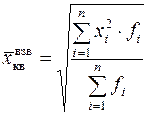 .
.
Пример. По данным табл. 4.5 рассчитать среднюю величину отклонений от заданной нормы.
Т а б л и ц а 4.5
Отклонение фактической длины изделия от заданной нормы ( 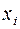 ), мм ), мм
| Число изделий ( 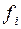 ), шт. ), шт.
|
| –1,8 | |
| –0,8 | |
| +0,2 | |
| +1,2 | |
| +2,3 | |
| Итого |
По исходным данным построим табл. 4.6.
Т а б л и ц а 4.6
Пример расчета средней квадратической взвешенной
Отклонение фактической длины изделия от заданной нормы ( 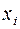 ), мм ), мм
| Число изделий ( 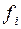 ), шт. ), шт.
| 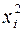
| 
|
| –1,8 | 3,24 | 3,24 | |
| –0,8 | 0,64 | 1,92 | |
| +0,2 | 0,04 | 0,16 | |
| +1,2 | 1,44 | 1,44 | |
| +2,3 | 4,84 | 4,84 | |
| Итого | ´ | 11,60 |
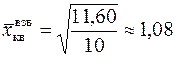 мм.
мм.
Средняя геометрическая – это величина, используемая как средняя из отношений или в рядах распределения, представленных в виде геометрической прогрессии. Этой средней удобно пользоваться, когда уделяется внимание не абсолютным разностям, а отношениям двух чисел. Поэтому средняя геометрическая используется в расчетах среднегодовых темпов роста.
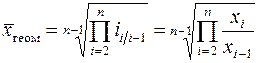 или
или 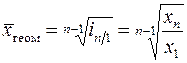 ,
,
где 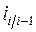 – относительная величина динамики цепная;
– относительная величина динамики цепная; 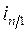 – относительная величина динамики базисная.
– относительная величина динамики базисная.
Пример. По данным табл. 4.7 определить среднегодовое увеличение выпуска товарной продукции за пять лет.
Т а б л и ц а 4.7
Дата добавления: 2015-08-01; просмотров: 783;
