Методические указания к выполнению задания по теме 4
Тема 4. Средние величины
Содержание задания и требования к нему
По теме 4 студент должен решить задачу, номер которой соответствует варианту.
Задача 1. Определить среднюю длительность операции.
| Длительность операции, с | 40–50 | 50–60 | 60–70 | 70–80 | 80–90 | 90–100 |
| Число операций |
Задача 2. Определить среднюю зарплату.
| Заработная плата, руб. | 2000– | 5000– | 8000– | 11000– | 14000– | 17000– |
| Число рабочих |
Задача 3. Определить среднюю скорость поезда.
| Скорость поезда, км/ч | 40–45 | 45–50 | 50–55 | 55–60 | 60–65 | 65–70 |
| Длина участка, км |
Задача 4. Определить средний процент брака.
| Процент брака | 0,5–1,0 | 1,0–1,5 | 1,5–2,0 | 2,0–2,5 | 2,5–3,0 |
| Выполненный объем работ, тыс. деталей |
Задача 5. Определить среднюю дальность поездки.
| Средняя дальность поездки, км | 60–65 | 65–70 | 70–75 | 75–80 | 80–85 | 85–90 |
| Удельный вес учтенных поездок, % к итогу |
Задача 6. Определить среднюю выработку рабочих.
| Выработка рабочего, шт./смену | 20–25 | 25–30 | 30–35 | 35–40 | 40–45 | 45–50 |
| Число рабочих |
Задача 7. Определить средний процент выполнения плана по отрасли.
| Процент выполнения плана | 90–100 | 100–110 | 110–120 | 120–130 | 130–140 |
| Объем выпуска продукции по плану, млн. руб. |
Задача 8. Определить средний процент выполнения плана.
| Процент выполнения плана | 85–90 | 90–95 | 95–100 | 100–105 | 105–110 |
| Фактический выпуск продукции, тыс. шт. |
Задача 9. Определить среднюю выработку деталей рабочим.
| Количество выработанных деталей одним рабочим в смену, шт. | ||||||
| Число рабочих, чел. |
Задача 10. Определить среднюю заработную плату.
| Зарплата рабочего в группе, руб. | |||||
| Фонд зарплаты по группе, тыс. руб. |
Методические указания к выполнению задания по теме 4
Средняя величина – это обобщающая количественная характеристика уровня варьирующего признака по однородной совокупности. Средние рассчитываются на основе массовых данных правильно статистически организованного массового наблюдения.
В зависимости от характера изучаемых явлений, от конкретных задач и целей статистического исследования применяются четыре вида средних:
– арифметическая;
– гармоническая;
– геометрическая;
– квадратическая.
Наиболее широкое применение и, следовательно, распространение имеет средняя арифметическая.
Средняя арифметическая может быть простой и взвешенной. Средняя арифметическая простая равна сумме произведений значений признака, деленной на их количество.
,
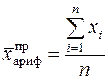где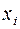 
– значение признака у i-ой единицы совокупности; 
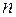– число единиц наблюдения в исследуемой совокупности.
Пример.По данным табл. 4.1 определить среднюю заработную плату рабочего бригады.
Т а б л и ц а 4.1
Дата добавления: 2015-08-01; просмотров: 1131;